Algoritmos de Atribuição Dinâmica de Tráfego

Para Atribuição Dinâmica de Tráfego, a demanda de tráfego é definida em termos de matrizes OD, cada uma fornecendo o número de viagens de cada centróide de origem para cada centróide de destino, para um intervalo de tempo e para um tipo de veículo. Quando um veículo é gerado em sua origem, é atribuído a um dos caminhos disponíveis, conectando essa origem ao destino do veículo. Esses caminhos são calculados quando a simulação começa e recalculados no intervalo de tempo de escolha de rota.

O veículo viajará ao longo desse caminho até seu destino, a menos que seja permitido atualizar dinamicamente a rota durante o percurso (ou seja, é um veículo guiado) e exista um melhor caminho da sua posição atual para o seu destino, ou seja desviado por uma ação de gestão de tráfego ou perca uma virada devido à congestão em simulações microscópicas. Veja mais informações sobre tipos de caminho aqui.

O processo de simulação para a Escolha de Rota Estocástica, baseado em caminhos dependentes do tempo, consiste nas seguintes etapas:

Etapa 0: Calcular árvores de caminhos mais curtos iniciais para cada centróide de destino usando os custos iniciais definidos.

Etapa 1: Simular por um intervalo de tempo predefinido (por exemplo, 5 minutos) conhecido como Intervalo de Escolha de Rota, atribuindo aos caminhos disponíveis a fração das viagens entre cada par OD para aquele intervalo de tempo, de acordo com o modelo de escolha de rota selecionado. Obter novos tempos médios de viagem do link como resultado da simulação.

Etapa 2: Recalcular os caminhos mais curtos, levando em conta os novos tempos médios de viagem do link e calcular a porcentagem de uso dos caminhos disponíveis.

Etapa 3: Se houver veículos guiados, fornecer as informações calculadas na etapa 2 para os motoristas que estão dinamicamente autorizados a atualizar o caminho durante o percurso.

Etapa 4: Voltar à etapa 1.

Esta seção descreve:

• Representação da Rede Rodoviária: Descrevendo como a rede de escolha de rotas é representada.
• Caminhos Definidos: Estes são caminhos fixos fornecidos pelo usuário ou de outro experimento.
• Funções de Custo do Link: Descrevendo como o custo percebido de atravessar uma seção de estrada é derivado.
• Caminhos Roteados: Descrevendo como os caminhos de rota são encontrados.
• Seleção de Caminho: Descrevendo como os veículos escolhem seus caminhos através da rede, incluindo o efeito de informações de sistemas ITS que fazem com que os veículos atualizem a escolha de caminho durante o percurso.

Representação da Rede Rodoviária

O uso de seções e interseções, a representação da rede e o detalhe usado para a simulação microscópica, são inadequados para os algoritmos de computação de caminhos. Isso requer uma representação em gráfico (links e nós) que considere explicitamente os movimentos de virada no final de uma seção e, portanto, o link que conecta dois nós usados nos cálculos de escolha de rota conterá tanto uma seção quanto um movimento de virada em termos de custo. Para converter de uma representação de seção de estrada e interseção para links, cada seção de estrada é dividida no mesmo número de links quanto existem movimentos de virada no final da seção; cada link pode então ser atribuído a um custo de atravessá-lo que inclui o custo atribuído à virada no final da seção.

A figura a seguir mostra um exemplo de uma rede de tráfego composta de seções e interseções. A representação da rede correspondente usada pelos algoritmos de rota, composta de nós e links, é mostrada abaixo. Note que, para cada seção, um nó é criado e há um link para cada movimento de virada. O custo atribuído a cada link é uma função de variáveis (como o tempo de viagem) da seção, mais variáveis do movimento de virada.

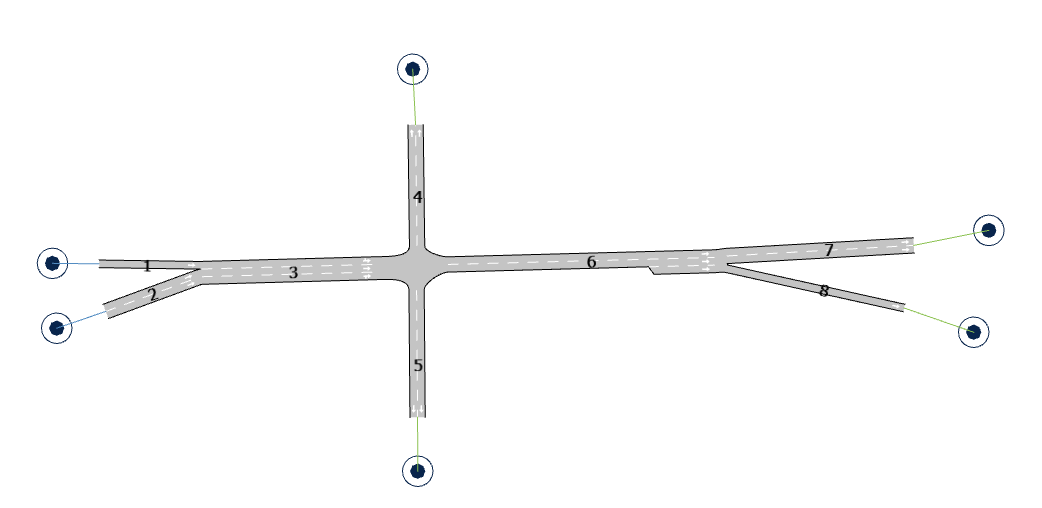
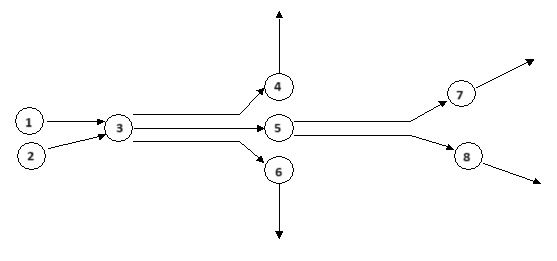
Caminhos Definidos

Os caminhos disponíveis de uma origem a um destino, que são levados em conta no processo de seleção de caminhos para o veículo, podem ser pré-definidos (rotas definidas pelo usuário ou rotas extraídas de árvores de caminhos mais curtos previamente calculados, ou soluções completas de escolha de caminho previamente calculadas) ou calculados aplicando um algoritmo de caminho mais curto, que usa os conceitos de "custo" e calcula árvores de caminhos mais curtos.

Rotas OD (anteriormente conhecidas como rotas definidas pelo usuário) correspondem à ideia de caminhos bem conhecidos, ou os caminhos mais familiares para os motoristas, de uma origem a um destino de acordo com o conhecimento do analista sobre a rede que está sendo modelada. Elas são pré-definidas pelo analista usando o editor de rede ou tomadas como saída de outros simuladores de tráfego ou modelos de transporte, sejam macroscópicos ou microscópicos.

As saídas da Atribuição de Caminhos são o resultado de uma atribuição de tráfego estática (macro) ou uma atribuição de tráfego dinâmica baseada em equilíbrio dinâmico do usuário usando microsimulação, mesoscopia ou simulação híbrida. A partir de uma atribuição de caminho, o usuário pode extrair rotas OD particulares ou todo o conjunto de árvores de caminhos mais curtos. As rotas OD são uma lista de links de uma origem a um destino, enquanto as árvores de caminhos mais curtos têm uma estrutura que define um caminho de cada link na rede até um destino. As duas estruturas, do ponto de vista lógico, representam um caminho ponto a ponto, mas na primeira representação, rotas OD, quando um veículo perde um movimento de virada, ele perde seu caminho e não tem mais informações. Com uma árvore de caminho mais curto, por outro lado, o veículo sabe como continuar seu caminho a partir do novo link.

Os caminhos mais curtos são calculados aplicando o algoritmo de caminho mais curto em uma rede representada como links e nós, na qual cada link tem uma função de custo associada que fornecerá o custo usado no cálculo do caminho mais curto.

Funções de Custo do Link

Na representação link-nó da rede usada no cálculo das rotas mais curtas, três diferentes tipos de funções de custo estão associadas a cada link e usadas para calcular as árvores de caminhos mais curtos, dependendo se dados simulados (ou seja, tempo de viagem simulado) estão disponíveis ou não. Elas são a função de custo dos caminhos mais curtos K-iniciais, a função de custo inicial e a função de custo dinâmica. Em todos os três casos, a ideia padrão da função de custo é que ela representa o tempo de viagem do link em segundos composto de um tempo de viagem da seção mais o tempo de viagem do movimento de virada; este último termo introduz a penalidade de tempo do movimento de virada no final do link. Outros termos como custos fixos e custos que dependem da atratividade dos links podem ser adicionados.

Os valores de custo do link têm uma faixa de valores possíveis \([1e-06..1e06]\). Todos os valores fora dessa faixa são substituídos, valores inferiores a \(1e-06\) são substituídos por \(1e-06\) e valores superiores a \(1e06\) são substituídos pelo custo máximo na faixa multiplicado por 10.

Para cada link, o usuário pode escolher a Função de Custo de Caminho Mais Curto K-Inicial, Função de Custo Inicial ou Função de Custo Dinâmica, e definir uma função de custo padrão de software (selecionando Padrão), ou selecionar qualquer outra função de custo definida pelo usuário. Isso é selecionado no editor de viradas, no quadro de lista de Funções de Custo da aba Modelos Dinâmicos encontrada dentro do Editor de Nós. As funções de custo são selecionadas na virada, pois a virada é o objeto único que diferencia links que compartilham a mesma seção de estrada.

Note que as Funções de Caminho Mais Curto K-Iniciais são usadas somente quando o cálculo de Caminho Mais Curto K-Inicial é usado.

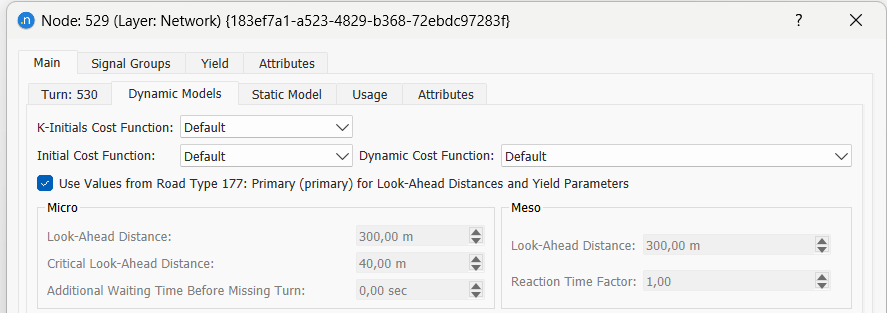
A lista de funções de custo disponíveis, e como estas são criadas e editadas, é descrita na Seção de Funções de Custo.

Atratividade do Link

A atratividade de um link pode ser definida no editor de nós na aba de Virada e aplicará a todos os links de roteamento que incluem a seção afetada.

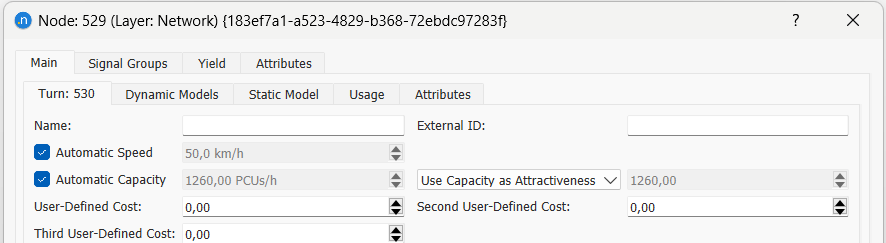
Entretanto, a rede pode calcular um valor de atratividade automatizada que se baseia em vários elementos: a capacidade de fluxo teórica das seções de origem e destino, o número de faixas nas seções envolvidas, o número de viradas com a mesma seção de origem e a capacidade de fluxo teórica dessas viradas.

Uma faixa tem um peso que denota sua contribuição para o cálculo da capacidade de um link. Por exemplo, uma faixa central faz uma contribuição completa para a capacidade de um link, mas uma saída ou uma faixa lateral tem um peso menor. Assim, o peso de uma faixa (WL_i) é definido como 1 para uma faixa central e 0,75 para faixa lateral ou de saída.

Algoritmo de Atratividade

A atratividade de um link – um link sendo uma seção (s) mais uma virada (t) – é obtida como resultado de um algoritmo que realiza os seguintes cinco passos:

1. Para cada virada considerada, encontra a atratividade desejada de cada virada que sai da seção de origem s (isso pode ser a capacidade necessária das faixas de destino ou a capacidade manual definida pelo usuário em t).

   A atratividade desejada é a quantidade teórica de atratividade que uma virada teria se a capacidade da seção de origem (s) fosse infinita. Mas a capacidade de origem é sempre finita e pode ser menor ou maior do que a atratividade desejada. Por exemplo, a seção de destino pode solicitar 1.000 PCUs e a faixa de origem pode ser capaz de fornecer 500 PCUs, ou até mesmo 2.000 PCUs.

   Nesses casos, o destino receberia 500 e 1.000 PCUs, respectivamente. Isso mostra que a atratividade desejada estabelece o limite superior e a origem fornece tanto quanto pode, até o valor do limite superior.
   2. Cada faixa de origem tem uma capacidade: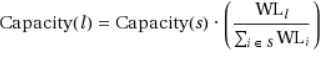

   

   Para cada virada de saída, o algoritmo subtrai a atratividade desejada dessa capacidade, levando em conta o peso de uma faixa.

   O resultado desse cálculo pode ser positivo ou negativo para uma faixa, significando que elas podem fornecer a capacidade desejada (usando a capacidade completa da faixa ou às vezes deixando a capacidade sobrante na faixa) ou têm um déficit (por exemplo, um destino deseja 1.000 PCUs, mas uma origem pode fornecer apenas 500 PCUs; isso criaria um déficit de 500).

   Para cada faixa em s, o seguinte cálculo se aplica:

   

   onde WL_i = peso da faixa l

   TLW = peso total de uma virada das faixas de origem

2. Após esse cálculo, o algoritmo determina quais faixas têm capacidade restante e quais estão em déficit (incapazes de fornecer a capacidade desejada). Rotula essas faixas de origem s como A e B:

   • Faixas Tipo A: esse tipo de faixa tem uma capacidade restante maior ou igual a 0, que é suficiente para fornecer a capacidade desejada de suas viradas e possivelmente ter alguma sobra.
   • Faixas Tipo B: esse tipo de faixa não pode fornecer a capacidade desejada. Pode precisar de 'ajuda' da capacidade remanescente de uma ou mais faixas tipo A.
3. Faixas tipo A redistribuem sua capacidade restante em excesso entre as faixas tipo B com as quais compartilham viradas.

4. Qualquer atratividade desejada que permanecer não atendida após essa redistribuição é corrigida. Isso é feito proporcionalmente entre as faixas de destino afetadas, usando o seguinte cálculo:

   

   onde E_l = capacidade desejada em excesso atribuída pela faixa

   R_l = a razão entre a capacidade ainda necessária da faixa l para a virada t e a capacidade total ainda necessária de l

As funções de custo do link devem sempre retornar um valor entre 0.000001 e 100000. Se a função de custo retornar um valor fora dessa faixa, o valor é substituído por um valor que assegura que os caminhos evitem usar este link. O valor de substituição é a soma de todos os custos de link para uma determinada classe de usuário, multiplicada por 10. Um aviso é exibido na janela de log para todos os pares de virada + classe de usuário que não retornam um custo entre a faixa predefinida.

Exemplo de Rede

A ilustração abaixo mostra parte de uma rede Aimsun. Ela compreende quatro seções (1, 2, 3 e 4) e uma interseção central que contém três viradas. Isso corresponde a três links na rede equivalente de escolha de rotas. A capacidade de cada seção é definida como rotulada.

Os números em azul indicam a capacidade real recebida por cada seção após a conclusão do algoritmo de cinco etapas explicado acima, levando em consideração redistribuições de capacidade e correções.

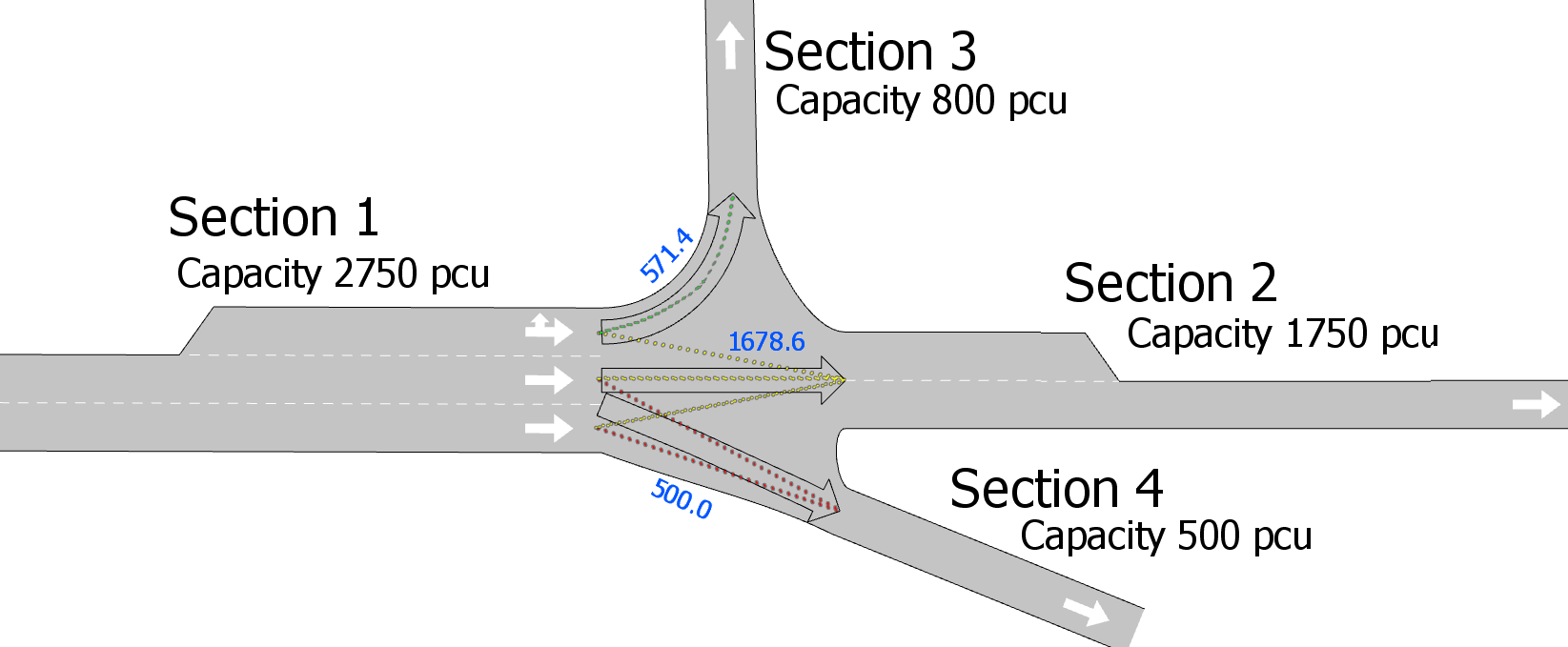
A capacidade das faixas na Seção 1 de origem (faixas 1.1, 1.2 e 1.3) é a seguinte. Note que a faixa 1.1 é uma faixa lateral com peso de 0.75.

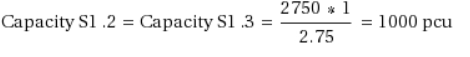
Neste exemplo, as cinco etapas do algoritmo prosseguem da seguinte forma.

1. A atratividade desejada por faixa é considerada:

   • Link 1: S3 requer 800 PCUs de S_1.1.
   • Link 2: S2 requer 1.750 PCUs no total: 477.27 de S_1.1 e 636.36 de ambas S_1.2 e S_1.3 devido aos diferentes pesos das faixas.
   • Link 3: S4 requer 500 PCUs no total: 250 de S_1.2 e S_1.3.

2. A atratividade desejada é subtraída da capacidade das faixas. A capacidade restante nas faixas de origem é:

   • Capacidade Restante S_1.1 = 750 – 800 – 477.27 = -527.27
   • Capacidade Restante S_1.2 = 1.000 – 636.36 – 250 = 113.64
   • Capacidade Restante S_1.3 = 1.000 – 636.36 – 250 = 113.64

3. As faixas de origem são rotuladas como A ou B:

   • As faixas S_1.2 e S_1.3 são faixas tipo A, com capacidade restante que pode ser compartilhada com a virada central S_1.1 (uma faixa tipo B).

4. A capacidade excedente é redistribuída para as faixas com déficit:

   • A capacidade de até 227.27 PCUs disponível em S_1.2 + S_1.3 que S_1.1 ainda precisa será compartilhada com ela pela virada S2, obtendo mais capacidade de S_1.2 e S_1.3, deixando as seguintes capacidades:
     • Capacidade Restante S_1.1 = -527.27 + 227.27 = -300
     • Capacidade Restante S_1.2 = S_1.3 = 0

5. Qualquer capacidade desejada em excesso é corrigida.

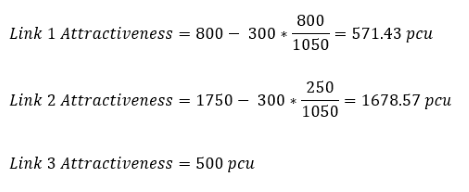
   • Isso é apenas necessário para viradas que têm capacidade de faixa negativa restante na origem:
     
     

Funções de Custo Inicial

A função de custo inicial é usada no início da simulação quando nenhum dado simulado ainda foi coletado e, portanto, os tempos de viagem experimentados não estão disponíveis. Neste caso, o custo padrão de cada link é calculado como uma função do tempo de viagem (em condições de fluxo livre), a atratividade do link e um custo fixo. O tempo de viagem em condições de fluxo livre é o tempo que um veículo levaria para atravessar o link, que é a seção mais a virada, assumindo que o veículo está viajando na velocidade máxima permitida ao longo da seção e na velocidade máxima de virada durante o movimento de virada. Nenhuma penalidade de tempo é incluída para sinais de trânsito.

Existem dois tipos de funções de custo inicial padrão. Para o primeiro tipo, \(IniCost_{j}\), o tipo de veículo não é levado em conta, ou seja, todos os tipos de veículos têm o mesmo custo inicial. Para o segundo tipo, \(IniCost_{j,vt}\), o tipo de veículo é considerado, o que significa que há uma função de custo inicial por tipo de veículo. Qual usar é determinado pela presença de faixas reservadas na rede ou tipos de veículos com diferentes velocidades desejadas em seções com limite de velocidade mais alto que a velocidade desejada dos tipos de veículos.

Se a penalidade para a virada \(t\) que pertence ao link for levada em conta, o custo padrão inicial do link \(j\), \(IniCost_{j}\), e sua atratividade, \(CL_{j}\), são calculados da seguinte forma:

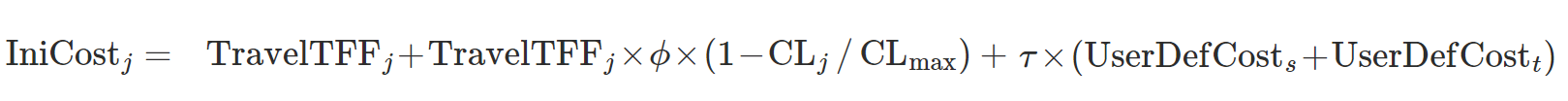
onde

• \(TravelTFF_{j}\) é o tempo de viagem estimado do link \(j\) em condições de fluxo livre.

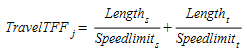
• φ é um parâmetro de peso de atratividade definido pelo usuário que permite ao usuário controlar a influência da atratividade do link no custo em relação ao tempo de viagem.

• \(CL_{max}\) é a atratividade máxima estimada teoricamente do link na rede.

• τ é um parâmetro de peso de custo definido pelo usuário que permite ao usuário controlar a influência dos custos definidos pelo usuário no custo do link.

• UserDefCost é o custo definido pelo usuário do link \(j\), que é a soma do custo definido pelo usuário da seção mais o custo definido pelo usuário da virada.

O custo padrão inicial do link \(j\) por tipo de veículo \(vt\), \(IniCost_{j,vt}\), é calculado da seguinte forma:

onde

• \(TravelTFF_{j,vt}\) é o tempo de viagem estimado do tipo de veículo \(vt\) no link \(j\) em condições de fluxo livre.

A diferença com o tempo de viagem em condições de fluxo livre, independentemente do tipo de veículo, é que a velocidade máxima média do tipo de veículo \(vt\), \(MaxSpeed_{vt}\) e a aceitação do limite de velocidade do tipo de veículo vt, θ\(_{vt}\). é usada para avaliar o tempo de viagem. Este último parâmetro (θ > 0) é o ‘nível de bondade’ dos motoristas ou o grau de aceitação dos limites de velocidade. Um valor de θ\(_{vt}\) ≥ 1 significa que o veículo adota uma velocidade máxima maior do que o limite de velocidade para a seção, enquanto θ\(_{vt}\) ≤ 1 significa que o veículo usará uma velocidade inferior ao limite de velocidade.

• \(Length_{j}\) é o comprimento do link \(j\) em quilômetros.
• φ é um parâmetro de peso de atratividade definido pelo usuário que permite ao usuário controlar a influência da atratividade do link no custo em relação ao tempo de viagem.
• \(CL_{max}\) é a atratividade máxima estimada teoricamente do link na rede.
• τ é um parâmetro de peso de custo definido pelo usuário que permite ao usuário controlar a influência do custo definido pelo usuário no custo total.
• \(UserDefCost\) é o custo definido pelo usuário do link \(j\), que é a soma do custo definido pelo usuário da seção mais o custo definido pelo usuário da virada.

Função de Custo Dinâmica

A Função de Custo Dinâmica é usada quando há dados simulados de tempo de viagem disponíveis. Portanto, ela só pode ser usada quando a simulação já começou e os dados foram coletados.

Assim como para a Função de Custo Inicial, também existem dois tipos de função de custo dinâmico padrão. A primeira, \(DynCost_{j}\) é aplicada a todos os tipos de veículos, o que significa que todos têm o mesmo custo. A segunda, \(DynCost_{j,vt}\), diferencia por tipo de veículo. Qual usar é determinado pela presença de faixas reservadas na rede ou tipos de veículos com diferentes velocidades desejadas em seções com um limite de velocidade mais alto do que a velocidade desejada dos tipos de veículos.

O custo padrão dinâmico para o link \(j\), comum a todos os tipos de veículos, \(DynCost_{j}\), é uma função do tempo médio de viagem, em segundos, para todos os veículos simulados que cruzaram o link durante o último período de coleta de estatísticas \(TravelTime_{j}\), mais um termo de atratividade e um custo fixo. O tempo de viagem para o link \(j\) inclui o tempo de viagem da seção s mais o tempo de viagem para o movimento de virada \(t\).

Pode haver situações em que nenhum veículo tenha cruzado um link, caso em que nenhuma informação sobre o tempo de viagem está disponível. O seguinte algoritmo é então aplicado para calcular \(EstimatedTravelTime_{j}\):

if (Flow > 0) then
    EstimatedTravelTime = TravelTime
else
    if (there is any vehicle stopped) then
        EstimatedTravelTime = AvgTimeInSection
    else
        EstimatedTravelTime = AverageSectionTravelTime
    endif
endif
EstimatedTravelTime = Maximum(EstimatedTravelTime, TravelFF)

De acordo com este algoritmo, quando alguns veículos cruzaram o link \(j\) durante o último período de coleta de dados (\(Flow_{j}\) > 0), o tempo de viagem estimado (\(EstimatedTravelTime_{j}\)) é tomado como o tempo médio de viagem simulado. Se nenhum veículo cruzou o link \(j\), devemos distinguir entre um link totalmente congestionado e um link vazio. No primeiro caso, o tempo de viagem é calculado como o tempo médio de espera para veículos aguardando na frente da fila na seção s (\(AvgTimeInSection_{s}\)). No segundo caso, o tempo de viagem é considerado como o tempo de viagem da seção, o que significa considerar todos os movimentos de virada que têm como origem a seção s (\(AverageSectionTravelTime_{s}\)). Todos os tempos de viagem calculados devem ser maiores ou iguais ao tempo de viagem do link em condições de fluxo livre.

Finalmente, o custo dinâmico do link \(j\), \(DynCost_{j}\), levando em conta a penalidade para a virada \(t\) que pertence ao link e sua atratividade, \(CL_{j}\) é calculado como:

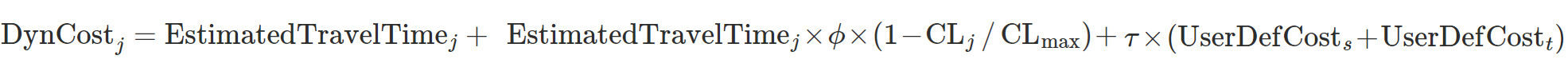
onde

• \(EstimatedTravelTime_{j}\) é o tempo de viagem estimado do link \(j\) calculado usando o algoritmo anterior.
• \(Length_{j}\) é o comprimento do link \(j\) em quilômetros.
• φ é um parâmetro de peso de atratividade definido pelo usuário que permite ao usuário controlar a influência que a atratividade do link tem no custo em relação ao tempo de viagem.
• \(CL_{max}\) é a atratividade máxima estimada teoricamente do link na rede.
• τ é um parâmetro de peso de custo definido pelo usuário que permite ao usuário controlar a influência do custo definido pelo usuário no custo total.
• \(UserDefCost\) é o custo definido pelo usuário do link \(j\), que é a soma do custo definido pelo usuário da seção mais o custo definido pelo usuário da virada.

O custo padrão dinâmico para o link \(j\) e tipo de veículo \(vt\): \(DynCost_{j,vt}\), é uma função do tempo médio de viagem, em segundos, para todos os veículos simulados do tipo \(vt\) que cruzaram o link durante o último período de coleta de dados (\(TravelTime_{j,vt}\)). O tempo de viagem para o link \(j\) inclui o tempo de viagem da seção s mais o tempo de viagem para o movimento de virada \(t\).

Pode haver situações em que nenhum veículo que pertença ao tipo de veículo \(vt\) tenha cruzado um link, caso em que nenhuma informação sobre o tempo de viagem está disponível, o seguinte algoritmo é então aplicado para calcular \(EstimatedTravelTime_{j,vt}\):

if (Flow(j,vt) > 0) then
    EstimatedTravelTime(j,vt) = TravelTime(j,vt)
else
    if (there is any vehicle vt stopped) then
        EstimatedTravelTime(j,vt) = AvgTimeIn(s,vt)
    else
        if (link j has reserved lanes of vehicle class cl) then
            if (vt belongs to cl) then
                if (FlowClass(j,cl) > 0) then
                    EstimatedTravelTime(j,vt) = TravelTimeClass(j,cl)
                else
                    if (there is any vehicle belonging to cl stopped) then
                        EstimatedTravelTime(j,vt) = AvgTimeInClass(s,cl)
                    else
                        EstimatedTravelTime(j,vt) = AverageSectionTravelTime(s,cl)
                    endif
                endif
            else
                if (FlowClass(j, not cl) > 0) then
                    EstimatedTravelTime(j,vt) = TravelTimeClass(j,not cl)
                else    
                    if (there is any vehicle not belonging to cl stopped) then
                        EstimatedTravelTime(j,vt) = AvgTimeInClass(s,not cl)
                    else
                        EstimatedTravelTime(j,vt) = AverageSectionTravelTime(s,not cl)
                    endif
                endif
            endif
        else
            if (Flow(v=j) > 0) then
                EstimatedTravelTime(j) = TravelTime(j)
            else
                if (there is any vehicle stopped) then
                    EstimatedTravelTime(j) = AvgTimeInSection(s)
                else
                    EstimatedTravelTime(j) = AverageSectionTravelTime(s)
                endif
            endif
        endif
    endif
endif
EstimatedTravelTime(j, vt) = Maximum(EstimatedTravelTime(j, vt),
TravelFF(j, vt)

De acordo com este algoritmo, quando um veículo do tipo \(vt\) cruzou o link \(j\) durante o último período de coleta de dados (\(Flow_{j,vt}\) > 0), o custo atual é tomado como o tempo médio de viagem simulado. Se nenhum veículo do tipo \(vt\) cruzou o link \(j\), devemos distinguir entre diferentes casos de custos calculados de acordo com os seguintes passos (cada etapa é realizada se nenhuma informação estiver disponível para a etapa anterior):

• \(AvgTimeIn_{s,vt}\) : Tempo médio de espera para o primeiro veículo do tipo de veículo vt na frente da fila na seção.

• Se a seção s tiver faixas reservadas para a classe de veículo \(cl\):

  • e o tipo de veículo \(vt\) usar a faixa reservada:
    • \(TravelTimeClass_{j,cl}\): É o Tempo Médio de Viagem do link \(j\) agregando todos os tipos de veículos da classe de veículo \(cl\).
    • \(AvgTimeInClass_{s,cl}\): É o tempo médio de espera para o primeiro veículo da classe de veículo \(cl\) na frente da fila na seção s.
    • \(AverageSectionTravelTime_{s,cl}\): É o tempo médio de viagem da seção de todos os veículos da classe de veículo \(cl\).
  • e o tipo de veículo \(vt\) não usar as faixas reservadas:
    • \(TravelTimeClass_{j,not\ cl}\): É o Tempo Médio de Viagem do link \(j\) agregando todos os tipos de veículos que não pertencem à classe de veículo \(cl\).
    • \(AvgTimeInClass_{s,not\ cl}\): É o tempo médio de espera para o primeiro veículo que não pertence à classe de veículo \(cl\) na frente da fila na seção s.
    • \(AverageSectionTravelTime_{s,not\ cl}\): É o tempo médio de viagem da seção de todos os veículos que não pertencem à classe de veículo \(cl\).

• Se a seção s não tiver faixas reservadas:

  • \(TravelTime_{j}\): É o Tempo Médio de Viagem do link \(j\) agregando todos os
  • tipos de veículos.
  • \(AvgTimeIn_{s}\): É o tempo médio de espera para o primeiro veículo na frente da
  • fila na seção s.
  • \(AverageSectionTravelTime_{s}\): É o tempo médio de viagem da seção para todos os tipos.

Todos os tempos de viagem calculados devem ser maiores ou iguais ao tempo de viagem do link em condições de fluxo livre.

Finalmente, o Custo Dinâmico do link \(j\) do tipo de veículo \(vt\): \(DynCost_{j,vt}\), considerando a penalidade para a virada t que pertence ao link e sua atratividade \(CL_{j}\), é calculado como:

onde:

• \(EstimatedTravelTime_{j,vt}\) é o tempo de viagem estimado do tipo de veículo \(vt\) do link \(j\) calculado com o algoritmo anterior.
• \(Length_{j}\) é o comprimento do link \(j\) em quilômetros.
• φ é um parâmetro de peso de atratividade definido pelo usuário que permite ao usuário controlar a influência que a atratividade do link tem no custo em relação ao tempo de viagem.
• \(CL_{max}\) é a atratividade máxima estimada teoricamente do link na rede.
• τ é um parâmetro de peso de custo definido pelo usuário que permite ao usuário controlar a influência do custo definido pelo usuário no custo total.
• \(UserDefCost_{s}\) é o custo definido pelo usuário do link \(j\), que é a soma do custo definido pelo usuário da seção mais o custo definido pelo usuário da virada.

Funções de Custo do Link Definidas pelo Usuário

As funções de custo padrão, descritas acima, são definidas em termos de tempo de viagem do link apenas e não consideram explicitamente outras influências, por exemplo, preços de pedágio, tempos de viagem históricos representando a experiência do motorista de dias anteriores, combinações de vários atributos numéricos de links, como por exemplo, tempos de viagem, tempos de atraso, comprimento e atratividade, etc. Portanto, para cada link, uma função de custo definida pelo usuário pode ser usada, que inclui esses atributos. Isso é criado com o editor de Função de Custo, conforme descrito na seção Funções.

As funções de custo definidas pelo usuário podem usar as funções e operadores matemáticos mais comuns (+ , -, *, /, ln, log, exp, etc.). Os termos da função podem ser definidos como parâmetros, constantes e variáveis, mas devem corresponder a atributos numéricos de um objeto no modelo (links, seções, viradas, tipos de veículos, etc.), cujos valores podem ser fixos (ou seja, comprimentos, capacidades teóricas, número de faixas, etc.) ou mudar durante a simulação (ou seja, fluxos de link, velocidades médias de link, tempos de viagem média de link, etc.).

Dois tipos de funções de custo definidas pelo usuário podem ser distinguidos: Funções de custo básicas (chamadas Função de Custo) e funções de custo considerando o Tipo de Veículo (chamadas Função de Custo com Tipo de Veículo).

As funções de custo básicas não distinguem entre tipos de veículos e, portanto, não podem fazer uso de variáveis que tenham qualquer referência de tipo de veículo. Os parâmetros para este tipo de função são: S (a referência da seção do link) e T (a referência da virada do link). As funções de custo considerando o Tipo de Veículo podem distinguir entre tipos de veículos e, consequentemente, podem fazer uso de variáveis derivadas do tipo de veículo. Os parâmetros para este tipo de função são: S (a referência da seção do link), T (a referência da virada do link) e a referência do tipo de veículo VT.

Se a função de custo definida pelo usuário considerar dados do tipo de veículo associados a qualquer link da rede, o cálculo de caminhos mais curtos é feito por tipo de veículo; caso contrário, é comum para todos os tipos de veículos.

Caminhos de Rota

Algoritmo de Caminho Mais Curto

Durante a simulação, os caminhos mais curtos são calculados a cada intervalo de tempo t (o Intervalo de Escolha de Rota). A rotina do caminho mais curto é uma variação do algoritmo de ajuste de rótulo de Dijkstra, Dijkstra (1959), e fornece como resultado a árvore de caminhos mais curtos para cada centróide de destino. Isso fornece o caminho mais curto do início de cada seção até aquele centróide de destino. Como isso inclui as penalidades de virada, os rótulos de custo são anexados a links em vez de a nós da rede.

A rotina do caminho mais curto baseia-se nas funções de custo do link. Portanto, os custos de todos os links são avaliados/atualizados antes que os caminhos sejam computados. No início da simulação, a função de custo inicial é avaliada para cada link e, durante os próximos intervalos de tempo, a função de custo dinâmica é usada.

A rotina de caminho mais curto gera uma árvore de caminho mais curto para cada centróide de destino d(\(SPT_{d}\), d ∈ D), mas há um passo extra que identifica novos caminhos para todos os pares OD i ∈ I, pegando \(SPT_{d}\), d ∈ D*, e adiciona ao conjunto de caminhos alternativos \(K_{i}\) do par OD \(i\). A partir de uma árvore de caminho mais curto, há tantos caminhos \(SP_{con}\) quanto conexões \(con\) para o centróide de origem.

O esquema genérico da Atribuição Dinâmica de Tráfego é:

Etapa 0: Calcular caminho(s) mais curto(s) iniciais para cada par OD usando os custos iniciais definidos.

Etapa 1: Simular por um intervalo de tempo predefinido (por exemplo, 5 minutos) atribuindo ao caminho disponível a fração das viagens entre cada par OD para aquele intervalo de tempo de acordo com o modelo de escolha de rota selecionado e obter novos tempos médios de viagem do link como resultado da simulação.

Etapa 2: Recalcular o caminho mais curto, levando em conta os tempos médios de viagem do link da simulação.

Etapa 3: Se houver veículos guiados, ou painéis de mensagens variáveis sugerindo uma mudança de rota, fornecer as informações calculadas na 2 para os motoristas que estão dinamicamente autorizados a atualizar o caminho durante o percurso.

Etapa 4: Voltar à etapa 1.

O algoritmo, incluindo os detalhes do cálculo do caminho mais curto, é o seguinte:

Etapa 0: Calcular caminho(s) mais curto(s) iniciais para cada par OD usando os custos iniciais definidos

• Etapa 0.1:Inicialização:
  • Avaliar a Função de Custo Inicial para cada link \(j\):
  • para cada \(j\) ∈ (1... \(L\)) :
    • \(Cost_{j}\) = \(InitialCost_{j}\)
• Etapa 0.2: Aplicar a rotina do Caminho Mais Curto:
  • para cada centróide de destino \(d\):
    • Calcular a Árvore de Caminho Mais Curto \(SPT_{d}\) usando \(Cost_{j}\) \(j\) ∈ (1... \(L\))
• Etapa 0.3: Identificar o Caminho Mais Curto da Árvore de Caminho Mais Curto:
  • para cada par OD \(i\) (do centróide de origem \(o\) para o destino \(d\))
    • Adicionar ao(s) Caminho(s) \(SP_{con}\) para \(K_{i}\)

Etapa 1: Simular por um intervalo de tempo predefinido Δ\(t\) atribuindo ao caminho disponível \(K_{i}\) a fração das viagens entre cada par OD \(i\) para aquele intervalo de tempo de acordo com o modelo de escolha de rota selecionado.

Etapa 2: Recalcular o caminho mais curto, levando em conta os tempos médios de viagem do link da experiência.

• Etapa 2.1: Atualizar Funções de Custo do Link:
  • Avaliar a Função de Custo Dinâmica para cada link \(j\):
  • para cada \(j\) ∈ (1... \(L\)) : \(Cost_{j}\) = \(DynamicCost_{j}\)
• Etapa 2.2: Aplicar a rotina do Caminho Mais Curto:
  • para cada centróide de destino \(d\):
  • Calcular a Árvore de Caminho Mais Curto \(SPT_{d}\) usando \(Cost_{j}\) \(j\) ∈ (1... \(L\))
• Etapa 2.3: Identificar o Caminho Mais Curto da Árvore de Caminho Mais Curto:
  • para cada par O-D \(i\) (do centróide de origem \(o\) para o destino \(d\))
    • Adicionar ao(s) Caminho(s) \(SP_{con}\) para \(K_{i}\)

Etapa 3: Se houver veículos que aceitam atualizar seu caminho durante o percurso, ou painéis de mensagens variáveis que sugerem atualizações de caminho por meio de ações de gestão de tráfego; fornecer as informações calculadas na etapa 2 aos motoristas que estão dinamicamente autorizados a atualizar o caminho durante o percurso.

Etapa 4: Voltar à etapa 1.

Os caminhos candidatos podem ser de três tipos diferentes (explicados na seção Definição de Caminho): Rotas OD (ODR), Resultado de Atribuição de Caminho (PAR) e Caminhos Mais Curtos Calculados, que podem ser calculados usando a Função de Custo Inicial Caminhos Mais Curtos Iniciais (ISP) ou calculados usando a Função de Custo Dinâmica, Caminhos Mais Curtos Dinâmicos (DSP).

Um veículo do tipo de veículo \(vt\) viajando do par OD \(i\), pode escolher um caminho de acordo com a atribuição definida pelo usuário ou como resultado de um modelo de Escolha de Rota do conjunto de caminhos alternativos \(K_{i}\):

• \(N\) Rotas OD: \(ODR_{n}\)^i^ \(n\)=1..\(N\)
• \(M\) Caminho de um resultado de Atribuição: \(PAR_{m}\)^i^ \(m\)=1..\(M\)
• \(P\) Caminhos Mais Curtos Iniciais: \(ISP_{p}\)^i^ , \(p\)=1..\(M\)
• \(Q\) Caminhos Mais Curtos Atualizados em Tempo Hábitos: \(DSP_{q}\)^i^, \(q\)=1..\(Q\)

Seleção Definida pelo Usuário

A seleção definida pelo usuário determina a probabilidade de uso para rotas OD e para resultados de atribuição de caminhos.

Para cada rota OD, o usuário determina a probabilidade de uso, distinguindo por tipo de veículo (definido na pasta "Atribuição de Caminho" na definição da matriz OD). O usuário define a probabilidade de uso de cada rota OD e a probabilidade de uso do caminho mais curto inicial:

\(P\)(\(ODR_{n}\)^i^, \(vt\)) : Probabilidade de uso \(ODR_{n}\)^i^ por um tipo de veículo \(vt\)

\(P\)($ISP_{p}^i^, \(vt\)) : Probabilidade de uso \(ISP_{p}\)^i^ por um tipo de veículo \(vt\)

Satisfazendo a condição:

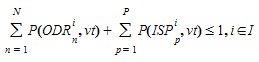
Aplicando uma atribuição de tráfego estática ou uma atribuição de tráfego dinâmica baseada em um experimento de Equilíbrio Dinâmico do Usuário, o resultado é um resultado de Atribuição de Caminho, que é um conjunto de caminhos (\(PAR_{m}\)^i^) e uma porcentagem de uso para cada um:

\(P\)(\(PAR_{m}\)^i^, \(vt\)) : Probabilidade de uso \(PAR_{m}\)^i^ por um tipo de veículo \(vt\)

Satisfazendo a condição:

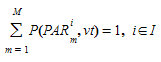
Modelos de Escolha de Rota

Em qualquer momento durante a simulação, haverá um conjunto finito de caminhos alternativos para cada par OD. A simulação da decisão do motorista de selecionar um dos caminhos disponíveis, ou seja, atribuir uma viagem a um caminho, é feita com um modelo de Escolha de Rota. Os modelos de Escolha de Rota geralmente são baseados na teoria das escolhas discretas que determina a probabilidade de escolher uma alternativa de um conjunto finito de alternativas como uma função de sua utilidade. Do ponto de vista de transporte, o valor mais comum associado a uma viagem é o tempo de viagem ou custo de viagem, que representa uma desutilidade. Portanto, os modelos de Escolha de Rota devem ser formulados em termos dessa utilidade negativa. O conceito mais comum de custo do caminho assume que é aditivo, então o custo do caminho \(I\), \(CP_{i}\), é calculado como a soma dos custos dos links \(Cost_{j}\) (explicado acima) que compõem o caminho:

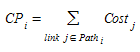
Os modelos de Escolha de Rota padrão disponíveis são: Proporcional, Logit Multinomial e C-Logit, mas outros também podem ser definidos usando o editor de funções.

Modo de Rotas Fixas Vs. Modo de Rotas Variáveis

No Modo de Rotas Fixas, as árvores de caminhos mais curtos são calculadas de cada seção para cada centróide de destino no início da simulação. Então, durante a simulação, os veículos são gerados nos centróides de origem e atribuídos à rota mais curta até seu centróide de destino. Não há necessidade de um Modelo de Escolha de Rota, pois não há rotas alternativas. Nenhuma nova rota é recalculada durante a simulação. Portanto, todos os veículos sempre seguem o caminho mais curto e não podem tomar decisões sobre mudar para outro caminho durante a viagem.

Dependendo do tipo de função de custo usada para os cálculos iniciais de caminhos mais curtos, existem dois modelos de rota fixa alternativos. Estes são o Fixado usando o Tempo de Viagem em Condições de Fluxo Livre (anteriormente identificado como Distância Fixa) e o Fixado usando o Tempo de Viagem durante o Período de Aquecimento (anteriormente identificado como Tempo Fixo).

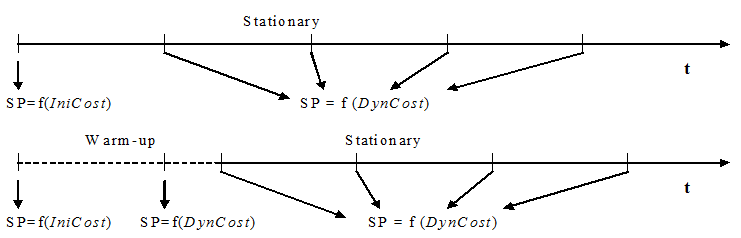
No Fixado usando o Tempo de Viagem em Condições de Fluxo Livre Modelo, os caminhos são calculados no início de uma simulação, tomando o custo inicial como custo de cada arco, esteja um período de aquecimento definido ou não. Se houver um período de aquecimento, nenhum novo caminho mais curto é calculado quando termina, portanto, as mesmas árvores de caminhos mais curtos são usadas durante o período de simulação estacionária. A próxima figura ilustra quando os caminhos mais curtos (SP) são calculados em um diagrama de tempo do período de simulação.

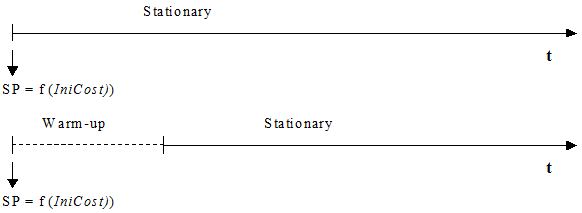
O Fixado usando o Tempo de Viagem durante o Período de Aquecimento Modelo funciona de maneira semelhante ao Fixado usando o Tempo de Viagem em Condições de Fluxo Livre, Modelo, exceto quando um período de aquecimento é definido. Nesse caso, os caminhos iniciais são calculados no início do Período de Aquecimento da mesma forma usando os Custos Iniciais. No entanto, quando o período de aquecimento termina e a simulação estacionária começa, novos caminhos iniciais são calculados usando a Função de Custo (calculada usando os dados estatísticos coletados durante o aquecimento da simulação) para os custos dos links. A próxima figura ilustra os cálculos de caminhos mais curtos (SP) em um diagrama de tempo do período de simulação.

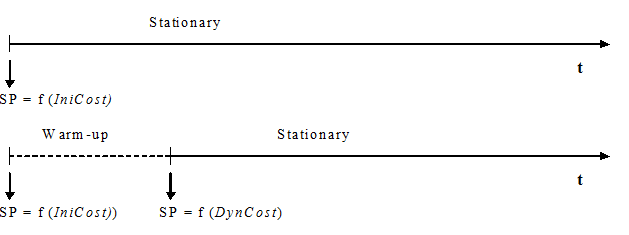
No Fixado usando o Tempo de Viagem em Condições de Fluxo Livre Modelo, o custo não leva em conta a congestão da rede, apenas o comprimento dos caminhos e a velocidade permitida. É rotulado como Fixado usando o Tempo de Viagem em Condições de Fluxo Livre Modelo para indicar que o custo é baseado principalmente nas distâncias, junto com os limites de velocidade e a atratividade, mas não nas condições de tráfego em um determinado momento. No Fixado usando o Tempo de Viagem durante o Período de Aquecimento Modelo, o custo é influenciado pelas condições de tráfego e, portanto, representa o tempo de viagem mais precisamente.

No modo de rotas variáveis, o processo de simulação inclui: um cálculo inicial das rotas mais curtas indo de cada seção a cada destino, um componente de rota mais curta que calcula periodicamente as novas rotas mais curtas de acordo com os novos tempos de viagem fornecidos pelo simulador, e um modelo de seleção de rotas.

No início da simulação, as árvores de caminhos mais curtos são calculadas de cada seção para cada centróide de destino, tomando como custos dos links a função de custo inicial, como no caso anterior. Se um período de aquecimento estiver definido, esses caminhos são calculados no início do aquecimento. Se não, eles são calculados no início do período de simulação estacionária.

Durante a simulação, novos caminhos são recalculados a cada intervalo de tempo, tomando como custos dos links os tempos de viagem simulados obtidos para cada arco durante o último intervalo. Essa é a função de custo explicada acima. A próxima figura ilustra quando os caminhos mais curtos (SP) são calculados durante o período de simulação e quais funções de custo são usadas.

O intervalo de tempo para a recalculação dos caminhos é definido no Editor de Experimentos. Presume-se que os veículos escolham apenas entre as melhores K árvores de caminhos. Esses K caminhos são os caminhos calculados nos intervalos anteriores mais as Rotas OD definidas nas matrizes OD. Apenas n Rotas OD serão adicionadas ao conjunto de possíveis caminhos. Esse parâmetro n é definido no Editor de Experimentos.

No momento atual, quatro modelos de escolha são implementados. Eles são usados seja ao atribuir o caminho inicial para um veículo no início de sua viagem ou ao decidir se deve mudar de caminho durante a simulação dinâmica. Esses modelos são os modelos Binomial, Proporcional, Logit Multinomial e C-Logit. Outros Modelos de Escolha de Rota podem ser definidos usando o Editor de Funções de Custo.

Atribuição Dinâmica

Quando uma matriz OD foi carregada em um modelo Aimsun, o experimento de simulação deve ser baseado em rotas. Antes de executar o modelo, qual tipo de Modelo de Escolha de Rota usar e os parâmetros são definidos na aba DTA do editor de experimentos.

Existem quatro modelos de escolha de rotas que requerem parâmetros para controlar o comportamento da rota para cada par OD, que são:

• Binomial: probabilidade.
• Proporcional: fator alpha.
• Logit: fator de escala.
• C-logit: fator de escala, beta e gama.

Os parâmetros são definidos na Subaba de Parâmetros da aba de Atribuição Dinâmica de Tráfego no Editor de Experimentos.

Modelo Binomial

Uma distribuição Binomial (\(k\)-1, \(p\)) é usada para encontrar a probabilidade de selecionar cada caminho. O parâmetro k é o número de caminhos disponíveis e p é a probabilidade de "sucesso". Este modelo não considera os custos de viagem no processo de decisão, mas apenas o tempo em que o caminho foi calculado. Selecionar um pequeno p significará que os caminhos mais antigos serão mais propensos a serem usados, enquanto selecionar altos valores de p fará com que os caminhos mais recentes sejam utilizados com mais frequência.

Por exemplo, se o objetivo é manter três caminhos alternativos e fazer com que os caminhos mais novos sejam usados com mais frequência, então defina \(k\)=3 e \(p\)=0.9. Então os valores possíveis para \(X\) = Binomial (2, 0.9) são \(X\) = 0,1,2 que estão respectivamente associados aos três últimos caminhos calculados. Suponha que o intervalo de tempo para recalcular os caminhos mais curtos seja de 5 minutos e o tempo de simulação atual seja 25:30. Nesse caso, os três últimos caminhos calculados foram calculados nos momentos 15:00, 20:00 e 25:00, correspondendo então \(X\) = 0 a 15:00, \(X\) = 1 a 20:00 e \(X\) = 2 a 25:00. Então, a probabilidade de selecionar o caminho mais antigo é \(P\)(\(X\)=0) = 0.01, a probabilidade de selecionar o segundo caminho é \(P\)(\(X\)=1) = 0.18 e a probabilidade de selecionar o caminho mais novo é \(P\)(\(X\)=2) = 0.81 (A próxima figura ilustra o modelo binomial com \(k\)=3 e \(p\)=0.9).

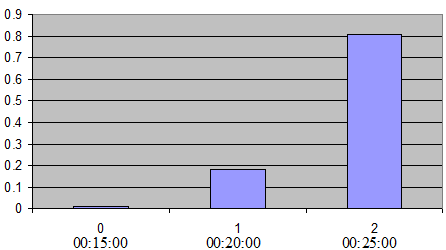
A probabilidade de 'sucesso' \(p\) pode ser definida via a aba de parâmetros do Experimento Editor quando o modelo Binomial é escolhido.

Proporcional

A probabilidade de escolha \(P_{k}\) de um determinado caminho alternativo \(k\), onde \(k\) ∈ \(K_{i}\), pode ser expressa como:

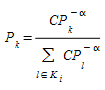
onde \(CP_{i}\) é o custo do caminho \(i\).

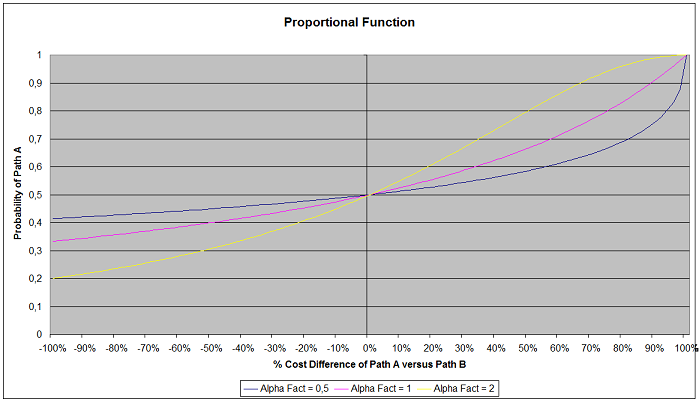
Quando α =1, a probabilidade é inversamente proporcional aos custos do caminho. A próxima figura mostra o papel do fator alpha, como uma função dos diferentes custos do caminho. O fator alpha pode, consequentemente, ser usado para ajustar o efeito que pequenas mudanças nos tempos de viagem podem ter sobre as decisões do motorista.

Logit Multinomial

A probabilidade de escolha \(P_{k}\) de um determinado caminho alternativo \(k\), onde \(k\) ∈ \(K_{i}\), pode ser expressa como uma função da diferença entre as utilidades medidas desse caminho e todas as outras rotas alternativas:

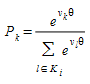
ou sua expressão equivalente:

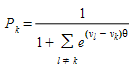
onde \(V_{i}\) é a utilidade percebida para o caminho alternativo \(i\) e θ é um fator de forma ou escala, e \(V_{i}\) = -\(CP_{i}\)/3600 (a função \(V_{i}\) é o negativo do custo do caminho \(i\), medido em horas).

Presumimos que a utilidade do caminho k entre