Métodos Estatísticos para Validação de Modelos

Os métodos e técnicas estatísticas para validar modelos de simulação são claramente explicados em muitos livros didáticos e artigos especializados Law e Kelton 1991, Balci 1998 e Kleijnen 1995. Esta seção demonstra a adaptação do processo geral para o problema da validação de um modelo de simulação dinâmica.

Os dados medidos da rede viária devem ser divididos em dois conjuntos de dados independentes: o conjunto de dados que será usado para desenvolver e calibrar o modelo e um conjunto de dados separado que será usado na validação. Esses dois conjuntos de dados podem ser dados diferentes (ou seja, calibrar o modelo com contagens de fluxo e de curvas, validá-lo com tempos de viagem) ou podem ser subconjuntos dos mesmos dados (ou seja, calibrar o modelo com um conjunto de fluxos, validá-lo com outro).

Em cada etapa de um processo iterativo de validação, um experimento de simulação será conduzido. Cada um desses experimentos de simulação será definido pelos dados de entrada do modelo de simulação e pelo conjunto de valores dos parâmetros do modelo que identificam o experimento. Esses serão ajustados para calibrar o modelo. A saída do experimento de simulação será um conjunto de valores simulados das variáveis de interesse, neste caso, os fluxos medidos em cada detector de tráfego na rede viária em cada intervalo de amostragem.

Por exemplo: assumindo que, no experimento de simulação, as estatísticas do modelo sejam coletadas a cada cinco minutos (o intervalo de amostragem) e que a variável amostrada seja o fluxo simulado \(w\). Então a saída do modelo de simulação será caracterizada pelo conjunto de valores \(w_{ij}\), do fluxo simulado no detector \(i\) no tempo \(j\), onde o índice \(i\) identifica o detector e o índice \(j\) o intervalo de amostragem. Se \(v_{ij}\) são as medidas reais correspondentes para o detector \(i\) no intervalo de amostragem \(j\), uma técnica estatística típica para validar o modelo seria comparar ambas as séries de observações para determinar se estão suficientemente próximas. Para cada detector \(i\), a comparação poderia ser baseada em testar se a diferença ao longo dos intervalos de tempo \(j\) (1 a \(m\)):

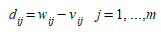
tem uma média significativamente diferente de zero ou não. Isso pode ser determinado usando a estatística t:

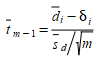
para testar a hipótese nula:

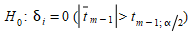
onde δ\(_{i}\) é o valor esperado de \(d_{i}\) e \(s_{i}\) é o desvio padrão de \(d_{i}\).

• Se para δ\(_{i}\) = 0 o valor calculado \(t_{m-1}\) da distribuição \(t\) de Student é significativo para o nível de significância especificado α, então temos que concluir que o modelo não está reproduzindo o comportamento do sistema de forma próxima e, portanto, temos que melhorar o modelo.

• Se δ\(_{i}\) = 0 resultar em um \(t_{m-1}\) não significativo, então concluímos que o modelo está reproduzindo adequadamente o comportamento do sistema e podemos aceitar o modelo.

Essa avaliação será repetida para cada um dos n detectores. O modelo é aceito quando todos os detectores, ou um subconjunto específico de detectores dependendo dos propósitos do modelo, passam no teste.

No entanto, no que diz respeito ao método estatístico, existem algumas considerações especiais a serem levadas em conta, especificamente no caso da análise de simulação de tráfego (Kleijnen 1995).

1. O procedimento estatístico assume observações idênticas e independentemente distribuídas (i.i.d), enquanto as medidas do sistema real e a saída simulada correspondente para uma série temporal podem não seguir essa suposição. Portanto, seria desejável que pelo menos as m diferenças pareadas (correlacionadas) \(d_{i}\) = \(w_{ij}\) – \(v_{ij}\), \(j\)=1,…,\(m\) sejam (i.i.d). Isso pode ser alcançado quando os \(w_{ij}\) e os \(v_{ij}\) são valores médios de experimentos replicados independentemente.

2. Quanto maior for a amostra, menor será o valor crítico 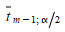, e isso implica que um modelo de simulação tem uma chance maior de ser rejeitado à medida que a amostra cresce. Portanto, as estatísticas t podem ser significativas e, ainda assim, não importantes se a amostra for muito grande, e o modelo de simulação pode ser bom o suficiente para fins práticos.

Essas considerações implicam que não é prudente confiar em apenas um tipo de teste estatístico para validar o modelo de simulação. Um teste alternativo é verificar se \(w\) e \(v\) estão positivamente correlacionados, ou seja, testar a significância da hipótese nula:

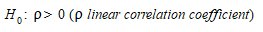
Isso representa um teste de validação menos rigoroso, aceitando que as respostas simuladas reais não necessariamente têm a mesma média e que o que é significativo é se elas estão positivamente correlacionadas ou não. O teste pode ser implementado usando a técnica de mínimos quadrados ordinários para estimar o modelo de regressão:

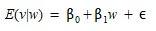
onde ε é um termo de erro aleatório.

O teste diz respeito à hipótese unilateral \(H_0\): β\(_1\) ≥ \(0\). A hipótese nula é rejeitada e o modelo de simulação aceito se houver forte evidência de que as respostas simuladas e reais estão positivamente correlacionadas. A análise de variância do modelo de regressão é a maneira usual de implementar esse teste. Este teste pode ser fortalecido, tornando-se equivalente ao primeiro teste se essa hipótese for substituída pela hipótese composta \(H_0\): β\(_0\) = 0, e β\(_1 = 1\), implicando que as médias das medições reais e das respostas simuladas são idênticas e quando uma medida do sistema excede sua média, então a observação simulada também excede sua média.

A comparação das duas séries \(v_{ij}\) e \(w_{ij}\) para intervalos de tempo \(j=1,...,m\) pode ser realizada com medidas de RMSPE (Erro Percentual Quadrático Médio), U de Theil ou a estatística GEH.

RMSPE

Se, para o detector \(i\), o erro de previsão no intervalo de tempo \(j\) (\(j=1,...,m\)) é \(d_{ij}\) = \(w_{ij}\) – \(v_{ij}\), então uma maneira comum de estimar o erro das previsões para o detector \(i\) é "Erro Percentual Quadrático Médio".

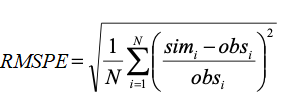
Essa estimativa de erro talvez tenha sido a mais utilizada em simulação de tráfego e, embora obviamente quanto menor for o valor de \(rmspe_i\), melhor será o modelo, ela tem um desvio significativo, pois eleva ao quadrado o erro, enfatizando assim grandes erros.

U de Theil

A estatística U de Theil (Theil 1966) é uma medida de associação entre duas séries, onde um valor de 0 implica que não há diferença entre os dados observados e os dados simulados e um valor de 1 implica que não há relação entre os dados observados e simulados.

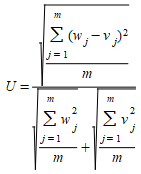
A U de Theil pode ser decomposta para quantificar três tipos diferentes de erro.

A Proporção de Viés \(U_m\) é uma medida do erro sistemático na simulação (a diferença líquida) e é definida como

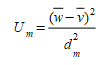
A Proporção de Variância \(U_s\) é uma medida da capacidade da simulação de reproduzir a variabilidade nos dados observados com base na diferença entre os desvios padrão nas duas séries e é definida como:

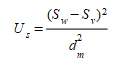
A Proporção de Covariância \(U_c\) é uma medida do erro não sistemático na simulação ou da falta de correlação entre as séries e é definida como:

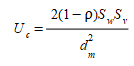
onde \(d^2_m\) é o erro médio de previsão ao quadrado (\(RMS^2\)) \(S_w\) e \(S_v\) são os desvios padrão amostrais das duas séries e ρ é o coeficiente de correlação amostral entre elas.

A melhor previsão é aquela onde \(U_m\) e \(U_s\) estão próximos de 0 e \(U_c\) está próximo de 1.

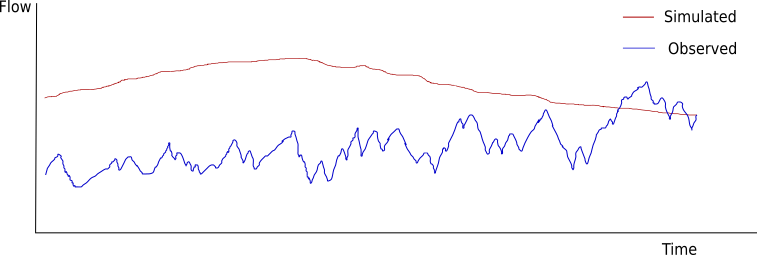
A figura abaixo demonstra um ajuste ruim por três razões:

1. A média das duas séries é diferente (\(U_m\)).
2. A variância nas duas séries é diferente (\(U_s\)).
3. A covariância é baixa (\(U_c\)), as subidas e descidas sistemáticas nos fluxos não estão correlacionadas.

GEH

A estatística GEH é usada para comparar volumes de tráfego. Seu nome é derivado de seu inventor Geoffrey E. Havers e é usada como um critério de aceitação para modelos de previsão de demanda de viagens pelas diretrizes do WebTAG do Reino Unido, onde um conjunto de limiares de aceitabilidade são fornecidos; um valor GEH inferior a 5 é considerado um bom ajuste, entre 5 e 10 implica que o local de medição merece investigação de erro e um valor superior a 10 implica um erro significativo e inaceitável. Como a medida é não linear, um único conjunto de limiares de aceitação pode ser especificado para uma ampla gama de valores de fluxo.

A estatística GEH é definida como:

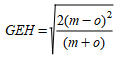
Onde m é o fluxo horário modelado e o é o fluxo observado.

GEH deve ser aplicado apenas a fluxos horários, ou fluxos ajustados a valores de 1 hora.

No Aimsun Next, a estatística discreta GEH classifica o valor GEH, principalmente para exibição e identificação de áreas problemáticas. Os valores são:

• GEH < 5: Bom ajuste - valor 0.
• GEH 5 - 10 E Observado < Resultado: Requer investigação, muito alto - valor 1.
• GEH > 10 E Observado < Resultado: Inaceitável, muito alto - valor 2.
• GEH 5 - 10 E Observado > Resultado: Requer investigação, muito baixo - valor 3.
• GEH > 10 E Observado > Resultado: Inaceitável, muito baixo - valor 4.