Reprogramação Dinâmica do Hora de Partida OD (HADES)¶
Uma das reações comuns que um viajante terá à congestão em uma rede de transporte é mudar seu horário de partida para garantir que ainda chegue ao seu destino no horário necessário. O efeito é espalhar a carga na rede de transporte e estender o período em que a rede opera em, ou perto da, capacidade máxima.
HADES¶
HADES (Horários Heterogêneos de Chegada e Partida com Programação de Equilíbrio) é um algoritmo desenvolvido em nome do Departamento de Transporte do Reino Unido. Ele modela a escolha microtemporária para o horário de chegada a um destino, onde as mudanças de horário são geralmente medidas em dezenas de minutos. O princípio por trás do HADES é que um viajante tem um horário de chegada preferido e que há um custo de programação associado a chegar cedo ou tarde. O viajante tentará então minimizar o custo total da viagem, incluindo o custo de programação, ajustando seu horário de partida.
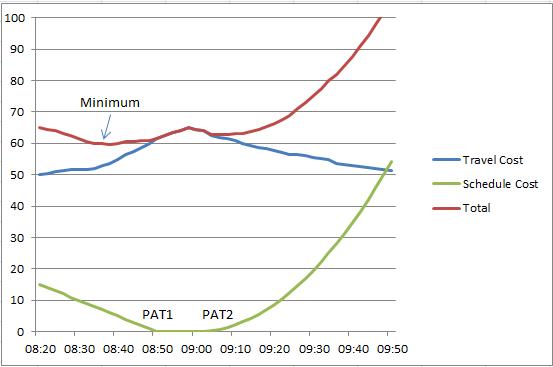
Por exemplo: Um viajante pode ter um Horário de Chegada Preferido (PAT) de 9:00 e um custo de viagem entre 50 e 65 minutos, onde um horário de chegada de 08:20 requer uma viagem de 50 minutos e um horário de chegada de 09:00 requer uma viagem de 65 minutos devido à maior congestão. Neste caso, o viajante associa um custo de programação de 0 por chegar até 10 minutos cedo, um custo de programação que cresce linearmente para chegar antes das 8:50 (PAT1 - Horário de Chegada Preferido 1) e um custo de programação que cresce exponencialmente para chegar depois das 9:00 (PAT2 - Horário de Chegada Preferido 2). Neste caso, como ilustrado abaixo, o momento ideal para o viajante chegar ao destino é 8:40 para minimizar o total dos custos de tempo de viagem e custos de programação.
O custo generalizado é, portanto:
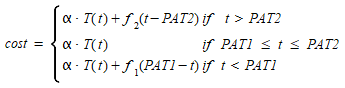
onde:
- \(t\): é o horário de chegada.
- \(PAT1\) e \(PAT2\) são o início e o fim da janela de horário de chegada.
- α: é um coeficiente de custo para a duração da viagem.
- \(T(t)\): é a duração da viagem para um horário de chegada t.
- \(f_1()\) e \(f_2()\) são funções de custo de programação para chegada antecipada e tardia, respectivamente.
Tempos de Viagem¶
Para cada iteração, à medida que o algoritmo HADES reatribui a demanda, um tempo de viagem é necessário, que variará de acordo com o horário de partida da viagem e fornecerá um perfil detalhado da mudança na duração da viagem ao longo do tempo. Esses tempos são derivados de um Equilíbrio Dinâmico de Usuários Mesoscópico que é executado usando um experimento DUE em cada iteração.
O HADES também requer tempos de viagem padrão para um conjunto de janelas de PAT para determinar o horário de partida em um cenário base para uma chegada em cada fatia do Horário de Chegada Preferido. Esses tempos são derivados de um arquivo .apa gerado a partir de um cenário base.
Custos de Programação¶
O custo de programação é derivado de uma Função que avalia o custo com base na diferença entre o horário de chegada e PAT1 e PAT2. Esta função pode ser uma função linear assimétrica simples que reflete a percepção de que chegar cedo tem um custo de programação menor do que chegar tarde, ou pode ser uma função exponencial que reflete a percepção de que a penalidade por chegar tarde se acumula mais rapidamente à medida que o atraso aumenta.
A função de custo de programação deve levar em conta a segmentação por Classe de Usuário e Finalidade da Viagem da viagem e também o horário do dia da viagem. Por exemplo, pode ser importante chegar ao trabalho antes das 9:00 e ajustar o horário de partida para alcançar isso, mas pode ser menos importante chegar em casa após o trabalho em um horário fixo e nenhuma reprogramação dinâmica do horário de partida OD seria necessária.
Iteração¶
Uma vez que os tempos de viagem iniciais foram determinados e os custos de programação programados, o Aimsun Next utiliza um processo iterativo para realocar a demanda entre os períodos de tempo usando um Método de Médias Sucessivas (MSA).
- Executar um DUE Meso para atribuir viagens à rede e derivar tempos de viagem.
- Calcular o custo de chegada em cada janela de horário de chegada.
- Atribuir a demanda de viagens a janelas de horário de chegada.
- Ajustar a demanda alocando viagens com um custo menor a uma janela de horário de chegada diferente e, portanto, um horário de partida diferente.
- Repetir até que os critérios de convergência sejam atendidos.
O ajuste da demanda é realizado usando um Método de Médias Sucessivas. Primeiro, para cada par OD e para cada segmento de demanda, a demanda é atribuída a:
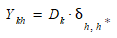
onde:
- \(k\) é a janela PAT preferida.
- \(h\) é a janela de chegada real.
- \(D_k\) é a demanda para uma combinação de par OD e classe de usuário com uma janela de horário de chegada alvo k.
- δ 1 se a viagem chega na janela de chegada \(h\) que corresponde à janela PAT \(h*\) com o menor custo combinado, 0 caso contrário.
- \(Y_{kh}\) é, portanto, a demanda por uma combinação de par OD e classe de usuário com uma janela alvo \(k\) que chega na janela \(h*\) que lhe dá o menor custo.
O algoritmo MSA então ajusta a demanda da seguinte maneira:
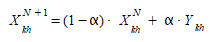
onde:
- \(X^{N}_{kh}\) é a demanda ajustada atual na iteração \(N\) para cada par OD e classe de usuário com uma janela de horário de chegada alvo \(k\) e janela de chegada \(h\).
- \(X^{N+1}_{kh}\) é a nova demanda ajustada na iteração \(N+1\).
- α é o comprimento do passo.
Convergência¶
Os critérios de convergência são baseados em uma função de intervalo delta agregada para cada par OD (\(i j\)) e classe de usuário (\(c\)):

onde \(C_{ijckh}\) é o custo de viagem para a viagem OD \(i-j\) para um veículo na classe \(c\) com uma janela PAT preferida \(k\) e uma janela de chegada real \(h\).