Equilíbrio Dinâmico do Usuário (DUE)¶

Para uma Atribuição Dinâmica de Tráfego se tornar um DUE, as suposições comportamentais sobre como os viajantes escolhem as rotas devem ser consistentes com o princípio de equilíbrio dinâmico do usuário. Ran e Boyce 1996 formulam a versão dinâmica do equilíbrio do usuário de Wardrop nos seguintes termos: Se, para cada par OD em cada instante de tempo, os tempos de viagem reais experimentados pelos viajantes que partem ao mesmo tempo são iguais e mínimos, o fluxo de tráfego dinâmico na rede está em um estado de equilíbrio dinâmico baseado no tempo de viagem (DUE).

Abordagem Heurística no Aimsun Next ¶

Essa formulação poderia corresponder aos cenários hipotéticos nos quais a aplicação de ATMS e ATIS operará e onde informações de tráfego confiáveis/sistemas de previsão de tráfego estarão disponíveis para os viajantes, permitindo que ajustem seu comportamento de acordo. Alternativamente, pode ser considerada como a realização de um processo no qual os viajantes ajustam suas informações atuais com conjecturas sobre as condições de tráfego esperadas à frente; isso poderia corresponder ao processo seguido pelos trabalhadores que adaptam seu comportamento com base em um processo de aprendizado dia a dia, dependendo das flutuações dos padrões de tráfego, até que considerem que nenhuma melhoria adicional é possível. Essa interpretação é implementada em uma abordagem de microsimulação por meio de um procedimento heurístico iterativo que imita o processo de aprendizado dia a dia levando a uma solução que pode ser interpretada como um DUE, Barcelo e Casas 2002, Liu et al. 2005.

A implementação no Aimsun Next replica a simulação $N$ vezes e os custos de link para cada link $j$, para cada intervalo de tempo $t, t+1, ..., L$ (onde $L = T/t$, $T$ sendo o horizonte da simulação e $t$ o intervalo de tempo definido pelo usuário no qual atualizar caminhos e fluxos de caminhos) em cada iteração $n$ são armazenados. Assim, na iteração $n$, os custos de link da iteração anterior $n-1$ podem ser usados para estimar o custo de link esperado na iteração atual. Seja $S_a^{jl}(v)$ o custo atual do link a com fluxo $v$, na iteração $l$ da replicação $j$, então os custos médios de link para os futuros $L-l$ intervalos de tempo, com base nos custos de link experimentados nas $j-1$ replicações anteriores, é dado por

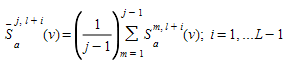
O custo de link "previsto" pode então ser computado como:

O custo resultante do caminho k para o i-ésimo par OD é dado por:

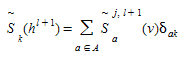
onde, como de costume, a matriz de incidência arco-caminho δ$_{ak}$ é: 1 se o link $a$ pertence ao caminho $k$ e 0 caso contrário.

Os custos de caminho são os argumentos da função de escolha de rotas (logit, C-logit, proporcional, definido pelo usuário, etc.) usados na iteração $l+1$ para dividir a demanda $g_i^{l+1}$ entre os caminhos disponíveis para o par OD $i$.

A implementação padrão na versão atual do Aimsun Next utiliza uma versão simplificada consistindo em uma função de custo de link definida como:

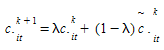
Onde $c_{it}^{k+1}$ é o custo usando o link i no tempo $t$ na iteração $k+1$, e $c_{it}^k$ e $c_{it}^k$ correspondem respectivamente aos custos de link esperados e experimentados neste intervalo de tempo de iterações anteriores.

Abordagens Algorítmicas para DUE ¶

Pode-se mostrar que a abordagem DUE pode ser implementada em termos de resolver o seguinte modelo matemático:

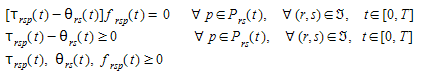
E as equações de balanceamento de fluxo

Onde, como antes, $f_{rsp}(t)$ é o fluxo no caminho $p$ de $r$ a $s$ partindo da origem $r$ no intervalo de tempo $t$, τ$_{rsp}(t)$ é o custo real do caminho de $r$ a $s$ na rota $p$ no intervalo de tempo $t$, θ$_{rs}(t)$ é o custo do caminho mais curto de $r$ a $s$ partindo da origem $r$ no intervalo de tempo $t$, $P_{rs}(t)$ é o conjunto de todos os caminhos disponíveis de $r$ a $s$ no intervalo de tempo $t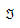$, é o conjunto de todos os pares origem-destino $(r,s)$ na rede e $d_{rs}(t)$ é a demanda (número de viagens) de $r$ a $s$ no intervalo de tempo $t$. Pode-se mostrar que isso é equivalente a resolver um problema de desigualdade variacional de dimensão finita consistindo em encontrar um vetor de fluxos de caminhos f* tal que:

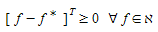
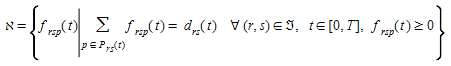
Wu et al. 1991, Wu et al. 1998a e 1998b, provam que isso é equivalente a resolver a desigualdade variacional discretizada:

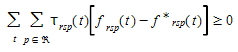
Onde 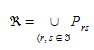é o conjunto de todos os caminhos disponíveis. Uma variedade de algoritmos foram propostos para resolver essa desigualdade variacional a partir de algoritmos de projeção: (Wu et al 1991, Wu et al. 1998a, Wu et al. 1998b, Florian et al. 2001) ou métodos de direções alternadas, Lo e Szeto 2002, para várias versões do Método de Médias Sucessivas (MSA), Tong e Wong 2000, Varia e Dhingra 2004, Florian et al 2002, Mahut et al. 2003a, Mahut et al. 2003b, e Mahut et al. 2004. O procedimento MSA redistribui os fluxos entre os caminhos disponíveis em um procedimento iterativo que na iteração n calcula um novo caminho mais curto da origem $r$ ao destino $s$ no intervalo de tempo $t$, $c_{rs}(t)$, então o processo de atualização dos fluxos de caminhos é:

Dependendo dos valores dos coeficientes de ponderação αn, diferentes esquemas de MSA podem ser implementados Carey e Ge 2007. Talvez o valor mais típico seja:

Um interessante algoritmo modificado de MSA é descrito em Varia e Dhingra 2004, onde o coeficiente de ponderação leva em conta um comprimento de passo variável que depende dos tempos de viagem atuais do caminho:

Um dos potenciais problemas computacionais nessas implementações de MSA é o número crescente de caminhos no caso de grandes redes; para evitar isso, no caso das atribuições DTA no Aimsun Next, o usuário tem a opção de especificar o número máximo K de caminhos a manter para cada par origem-destino, portanto, ao implementar o MSA no Aimsun Next, considerou-se que seria desejável manter esse recurso.

Várias implementações modificadas de MSA foram propostas para manter controle sobre o número de caminhos em algoritmos MSA, Peeta e Mahmassani 1995, Sbayti et al. 2007, no entanto, possivelmente uma das mais eficientes computacionalmente é a proposta por Florian et al. 2002 (veja também Mahut et al. 2003b e 2004) modificando o algoritmo MSA para manter o número de caminhos alternativos contidos para cada par origem-destino. Esta variante do algoritmo inicializa o processo com base em um esquema de carga incremental distribuindo a demanda entre os caminhos mais curtos disponíveis, o processo é repetido por um número predeterminado de iterações, após o qual nenhum novo caminho é adicionado e a fração correspondente da demanda é redistribuída de acordo com o esquema MSA. O MSA modificado funciona da seguinte forma:

Deixe K ser o número máximo de iterações para calcular novos caminhos:

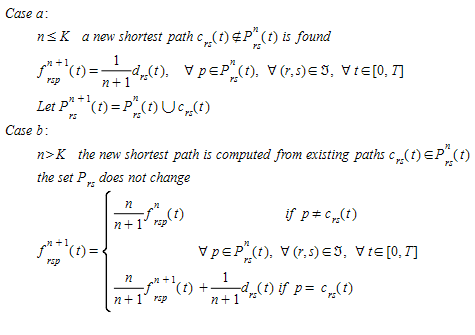
Esta é a versão do algoritmo MSA implementada no Aimsun Next. No entanto, levando em conta a possibilidade de repetir caminhos mais curtos de uma iteração para a próxima para manter um máximo de K diferentes caminhos mais curtos, uma implementação adequada do algoritmo requer que o número de iterações n seja definido por par OD e intervalo de tempo.

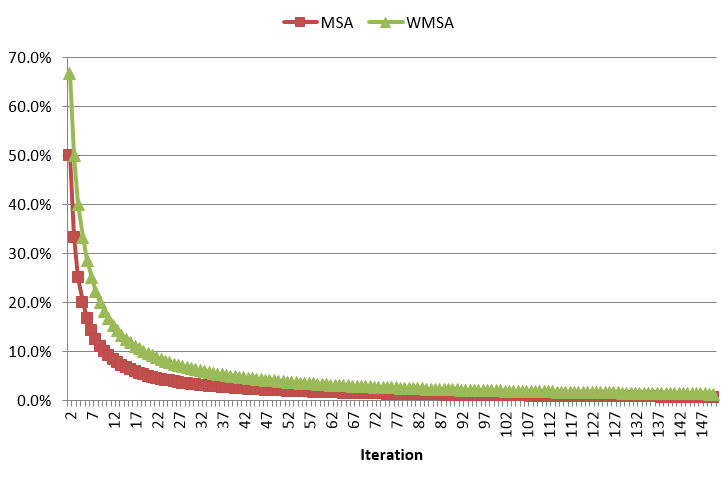
No Aimsun Next, uma modificação do algoritmo MSA está disponível chamada WMSA proposta por Liu et al. 2007. O algoritmo MSA na iteração n, 1/n da demanda é movido, e no WMSA 2/(n+1) da demanda é movido. A próxima figura mostra a quantidade de demanda movida em função do número de iteração.

Demanda movida em função do número de iteração usando MSA e WMSA

O critério de convergência ¶

Todas as abordagens propostas para DUE são baseadas em procedimentos de simulação para o processo de carga da rede e, portanto, são heurísticas por natureza, de modo que nenhuma prova formal de convergência pode ser fornecida. Consequentemente, uma maneira de determinar empiricamente se a solução alcançada pode ser interpretada em termos de um DUE, no sentido de que "o tempo de viagem real experimentado pelos viajantes que partem ao mesmo tempo é igual e mínimo", pode ser baseada em uma versão ad hoc da função Gap Relativo proposta por Janson 1991:

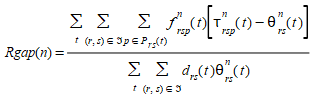
Onde

$f_{rsp}^n(t)$ é o fluxo no caminho p partindo da origem $r$ no tempo $t$ na iteração $n$ com destino s.
τ$_{rsp}^n(t)$ é o custo experimentado ou instantâneo do caminho p.
θ$_{rs}^n(t)$ é o custo do caminho mais curto para caminhos partindo da origem r no tempo t na iteração n com destino s.

A diferença τ$_{rsp}^n(t)$ - θ$_{rs}^n(t)$ mede o custo excessivo experimentado pelo fato de usar um caminho p em vez do caminho mais curto.

Nas versões anteriores, o custo do caminho mais curto na fórmula RGap para caminhos partindo da origem θ$_{rs}^n(t)$ era o da caminho com o menor custo entre o conjunto de caminhos utilizados. A partir do Aimsun Next 22, esse é o custo do novo caminho mais curto calculado com os custos atualizados ao final da iteração.

Isso é mais preciso e permite uma melhor avaliação do RGap para pares OD em que todos os veículos usam o mesmo caminho. No entanto, você pode observar que o RGap no Aimsun Next 22 é maior e que o DUE realiza mais iterações para convergir. Se isso lhe preocupa, você ainda pode usar o cálculo anterior adicionando uma nova variável de experimento com o nome $DTARGAPEVALUATION e um valor de RGAP20.

A razão mede o custo total excessivo em relação ao custo mínimo total se todos os viajantes tivessem usado caminhos mais curtos.

Como critério de parada, um Gap Relativo global padrão pode ser definido na aba de Atribuição Dinâmica de Tráfego do editor de experimentos para um número específico n de iterações consecutivas (por padrão, n = 1). Uma matriz de gap relativo com diferentes limites também pode ser definida para cada par OD. Quando uma Matriz de Gap Relativo é definida, para aqueles pares OD com um valor maior que 0, o limite OD local é usado, caso contrário, o processo DUE usa o gap relativo global.

No processo DUE com gap relativo global, há a possibilidade de incluir outros dois critérios de convergência adicionais:

Uma porcentagem x% de links com uma alteração de fluxo abaixo de y% por pelo menos n iterações consecutivas (por padrão n = 4).
Uma porcentagem x% de links com uma alteração de custo abaixo de y% por pelo menos n iterações consecutivas (por padrão n = 4).

Esses dois critérios adicionais estão desativados por padrão e podem ser ativados individualmente na aba de Atribuição Dinâmica de Tráfego do editor de experimentos. Uma vez ativos, a convergência é alcançada quando ambos os critérios de gap e os critérios de fluxo/custo são atendidos, ou quando o número máximo de iterações é alcançado.

A estrutura computacional no Aimsun Next ¶

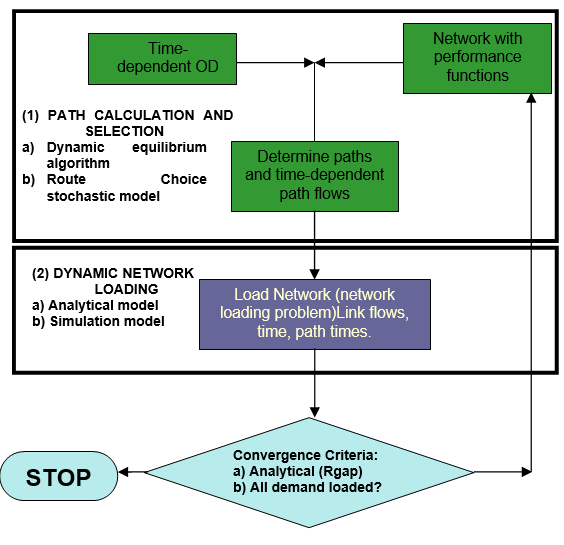
A estrutura computacional para DTA proposta por Florian 2001 e Florian 2002 consiste em dois componentes:

Um método para determinar as taxas de fluxo dependentes do caminho nas rotas na rede
Um método de Carga de Rede Dinâmica, que determina como esses fluxos de caminho dão origem a volumes de arco dependentes do tempo, tempos de viagem de arco e tempos de viagem de caminho.

Isso foi implementado no Aimsun Next, como mostrado no diagrama conceitual abaixo. Quando o diálogo de Cenário Dinâmico é selecionado, o sistema oferece três opções: microscópico, mesoscópico e híbrido, que determinam a abordagem de simulação sobre a qual a carga da rede é baseada; e para cada carga da rede, duas alternativas são oferecidas: DTA ou DUE.

DTA é baseada na abordagem heurística descrita usando modelos estocásticos de escolha de rotas.
DUE é baseada na heurística iterativa descrita acima e em algoritmos MSA ou baseados em gradiente.

Os critérios de convergência dependem da alternativa selecionada: a conclusão da carga de demanda no DTA e seja a conclusão do número de iterações definidas ou quando a função Rgap atinge a precisão desejada.

Uma implementação computacional eficiente dessa abordagem conceitual requer que a parte analítica do processo, ou seja, o cálculo e seleção de caminhos, seja implementada independentemente do processo de carga dinâmica da rede selecionada para implementar a parte heurística da Atribuição Dinâmica de Tráfego. Em outras palavras, quando a consistência da rede se mantém para a representação meso e micro, o cálculo do caminho baseado em custos de link dependentes do tempo deve ser o mesmo e a única diferença dependerá dos valores dos argumentos das funções de custo de link que serão fornecidos, respectivamente, pela simulação de tráfego mesoscópica ou pela simulação de tráfego microscópica usados para a Carga de Rede Dinâmica.

Diagrama conceitual da atribuição dinâmica heurística

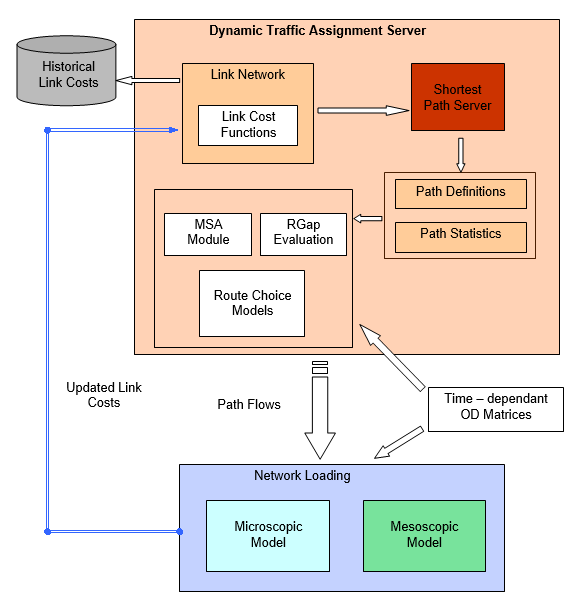
A arquitetura de software integrada do Aimsun Next permite tal cálculo comum de caminhos mais curtos, dado que as representações da rede compartilham o mesmo modelo de objeto e banco de dados de modelo e veículos podem ser únicos e os mesmos para meso e micro se o modelo meso for baseado em uma abordagem que individualiza veículos, então o cálculo de caminho pode ser realizado por um "servidor de caminho mais curto" comum e são os mesmos em ambos os níveis. A abordagem conceitual para a atribuição dinâmica de tráfego proposta na figura anterior foi implementada em termos de um "Servidor de Atribuição Dinâmica de Tráfego". A estrutura deste servidor é mostrada abaixo.

Estrutura do Servidor de Atribuição Dinâmica de Tráfego

Parâmetros DUE ¶

Antes de executar o modelo, os parâmetros do Equilíbrio Dinâmico do Usuário são definidos nas propriedades do Experimento na aba de Atribuição Dinâmica de Tráfego.

Estimativa das taxas de fluxo de caminhos ¶

A nova abordagem implementa a estimativa das taxas de fluxo de caminhos baseadas em um Equilíbrio Dinâmico do Usuário (DUE). Este processo implementa um processo iterativo para minimizar o Gap Relativo aplicando o método das médias sucessivas (MSA),

Iniciar e Continuar um Equilíbrio Dinâmico do Usuário ¶

Continuar ou iniciar um DUE a partir de um DUE anterior ou uma Atribuição Macro usando um arquivo APA é possível, independentemente de a rede ter sido alterada ou não. A primeira iteração ao iniciar ou continuar um DUE usando uma atribuição anterior é utilizada para calcular os custos de link. Se a rede foi alterada, o fixador APA pode ser usado para garantir que a rede e o arquivo APA sejam consistentes. O fixador APA verifica um arquivo APA e o "corrige" com base na configuração atual da rede para que ele possa ser usado em uma versão modificada da rede. Isso contorna a restrição de que os caminhos podem ser específicos apenas para uma versão da topologia da rede. O fixador APA implementa as seguintes mudanças:

Adição e remoção de centróides e/ou conexões
Adição, remoção ou modificação de definições de viradas e/ou de entidades de conexão de viradas
Adição, remoção ou modificação de seções

O fixador APA é uma ferramenta de linha de comando que recebe como entrada:

O arquivo APA original
A rede revisada
O identificador para o experimento na rede revisada.

O novo arquivo APA é enviado para um novo diretório "correctedapa" localizado no mesmo diretório que o APA original.

Nos três casos, o fixador APA assegura que o arquivo APA resultante será compatível com a nova rede e garantirá que a atribuição anterior seja consistente. Assim, para cada origem e destino, a atribuição soma 100%.

Resultado Incremental ¶

Com o objetivo de melhorar o processo geral de convergência e obter melhores rotas, pode-se utilizar um resultado incremental. A diferença entre um resultado normal e um resultado incremental é o número de iterações externas. Em um resultado normal, há apenas uma iteração externa usando a demanda definida no cenário. Em um resultado incremental, o usuário pode especificar um número de iterações externas com diferentes porcentagens crescentes. A porcentagem de cada iteração externa define a proporção da demanda que será utilizada. As primeiras iterações têm demanda menor e essa demanda é aumentada a cada iteração externa com 100% da demanda na última iteração.

O objetivo é desenvolver roteamento em uma rede descongestionada para evitar a distorção no roteamento causada por supercongestão na simulação.