Planejamento de Transporte e Modelos e Algoritmos de Análise de Demanda no Aimsun Next

O Modelo de Quatro Etapas no Planejamento de Transporte

A demanda de viagens urbanas e a análise de mobilidade evoluíram para uma metodologia bem estabelecida, comumente chamada de modelo de quatro etapas.

Esta seção descreve os Modelos de Planejamento de Transporte e Análise de Demanda implementados no Aimsun Next e os algoritmos que utilizam. É composto pelas seguintes seções:

• Arquitetura do Sistema
• Zonas
• Rede
• Geração de Viagens
• Distribuição de Viagens
• Atribuição Estática
• Ajuste Estático

Arquitetura do Sistema

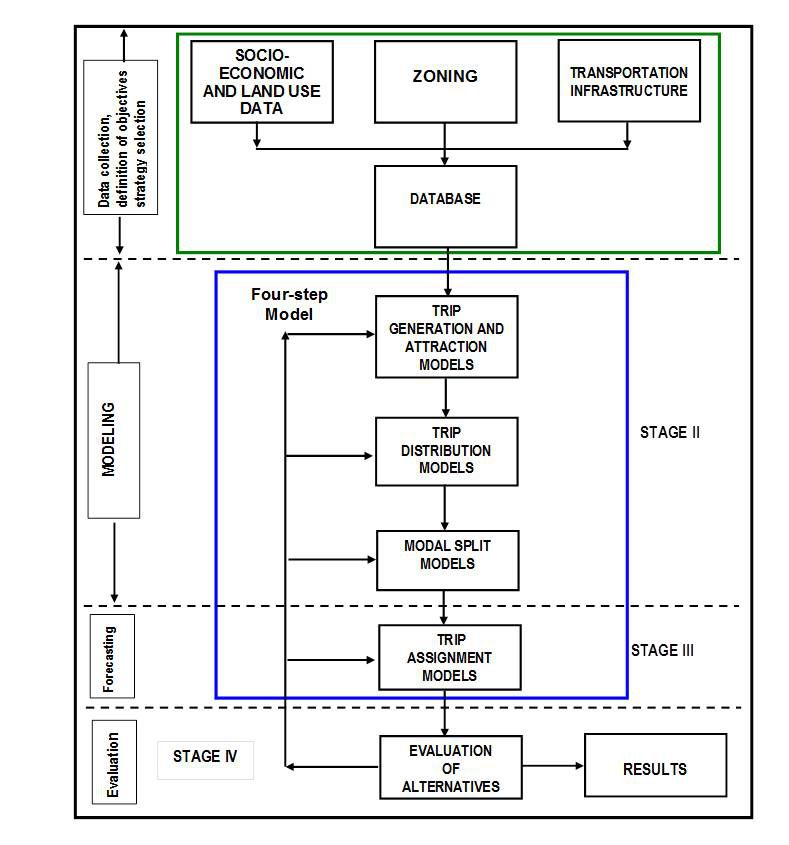
Ortúzar e Willumsen (2001) propõem uma metodologia geral conceitualmente representada no diagrama abaixo, que incorpora o modelo clássico de quatro etapas. A abordagem metodológica consiste nas seguintes etapas:

• Etapa I:

  Os objetivos do estudo são definidos, as estratégias para atingir esses objetivos são selecionadas e os dados necessários para conduzir o estudo são coletados. Isso geralmente implica:

  • A coleta de dados socioeconômicos e de uso do solo, geralmente estruturados de acordo com um esquema de zoneamento que divide a área objeto do estudo.
  • A coleta de todas as informações referentes à infraestrutura de transporte: autoestradas, rodovias, estradas, ruas e vias urbanas, linhas de transporte público, ferrovias, etc.

• Etapa II:

  Esta é a etapa de modelagem e contém três dos quatro passos do modelo de quatro etapas: - A construção dos modelos de Geração e Atração de Viagens (Passo I) - A construção dos modelos de Distribuição de Viagens (Passo II) - A construção dos modelos de Divisão Modal (Passo III)

• Etapa III:

  A etapa de previsão, também conhecida como Modelos de Atribuição de Viagens. Este é o Passo IV do modelo de transporte de quatro etapas.

• Etapa IV:

  A etapa de avaliação; os resultados da previsão são analisados e avaliados usando os critérios identificados na etapa I. Os resultados são reportados e entregues aos tomadores de decisão.

Processo

A metodologia, como representada no diagrama, com o Modelo de Quatro Etapas destacado na caixa azul, deve ser entendida como um processo iterativo no qual os resultados de qualquer etapa podem levar à reavaliação das etapas anteriores, ou a uma necessidade de novos dados ou evidências para refinamento das etapas anteriores.

As ferramentas e algoritmos de modelagem nos componentes de planejamento de transporte e análise de demanda no Aimsun Next foram projetados para apoiar o analista de transporte na aplicação das funções mais relevantes do modelo de quatro etapas.

Zonas

A análise de transporte é conduzida com modelos cujos componentes são:

• A infraestrutura e os serviços de transporte: ou seja, a rede viária, transporte público, etc.
• As políticas de operação e controle do sistema de transporte.
• A demanda por viagens, incluindo padrões de atividade e uso do solo, ou seja, o esquema de zonas.

Viajar é uma atividade que ocorre ao se mover de uma localização a outra em uma rede de transporte (Oppenheim, 1995). Assim, a maioria dos conceitos usados na modelagem de sistemas de transporte tem uma dimensão espacial e a primeira questão a ser abordada é como representar a estrutura espacial.

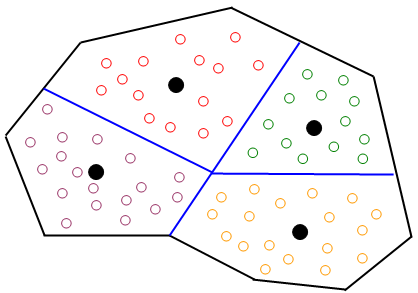
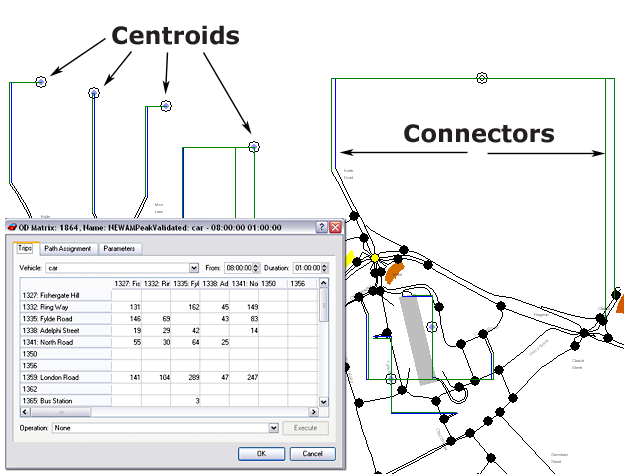
A abordagem tradicional é usar um conjunto de zonas agregadas, nas quais as localizações dos viajantes são agrupadas em "zonas de tráfego" definidas pelo analista. O tamanho de cada zona de tráfego pode variar de um quarteirão da cidade a um bairro inteiro ou uma cidade, dependendo dos requisitos do modelo. Cada zona de tráfego é representada por um nó "centroide" (localizado geralmente no centro geométrico ou de gravidade da zona). A estrutura espacial abstraída correspondente a uma determinada estrutura geográfica pode ser visualizada em uma área hipotética como na figura abaixo, na qual cada ponto branco representa uma localização individual do viajante e pontos pretos os centroides das zonas. No processo de planejamento de transporte, a representação típica da demanda consiste em uma partição da área em estudo em zonas de tráfego. A chave para uma modelagem bem-sucedida é determinar o número e o tamanho apropriados dessas zonas.

Rede

A infraestrutura de transporte é modelada em termos de um gráfico \(G=(N,A)\), cujos nós \(i_N\) representam tanto "centroides", ou seja, as fontes ou origens de viagens e os pontos de destino dessas viagens, ou representam interseções. As ligações a∈A representam a infraestrutura física, ou seja, os trechos de estrada ou rua urbana entre interseções, e existem "ligações fictícias", também chamadas de "conexões", cuja função é conectar fisicamente os nós de origem e destino ao gráfico que modela a rede viária. O gráfico pode ser interpretado como uma abstração da rede viária física.

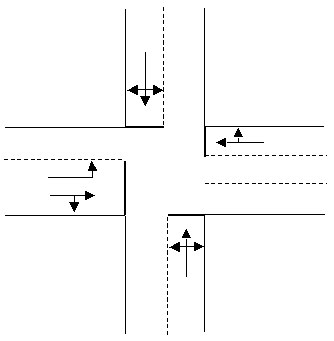
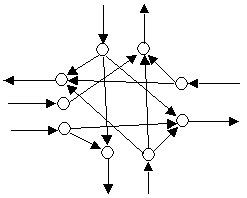
Quando uma rede viária é representada como um gráfico abstrato, como para modelagem de atribuição estática. Existem um conjunto de regras que devem ser seguidas para fornecer uma representação realista, ou seja, as interseções devem ser representadas em termos de subgráficos que modelam os movimentos permitidos e as penalidades por conversão estão associadas a esses movimentos para representar os atrasos na rede viária. A figura abaixo mostra um exemplo de interseção representada como um layout físico e como uma rede abstrata.

Aimsun Next fornece três classes principais de objetos para apoiar o processo de modelagem em quatro etapas:

• Os trechos de estrada e nós são usados para descrever a rede.
• Os centroides e conexões descrevem as zonas e as ligam à rede viária.
• Uma Matriz de Viagens T descreve a demanda de tráfego onde as entradas \(t_{ij}\) representam o número de viagens com origem na zona i e destino na zona j.

Aimsun Next fornece ferramentas para criar, editar e vincular esses objetos para formar um modelo de transporte.

A figura abaixo mostra um exemplo de matriz OD para a rede do exemplo, na qual os nomes das linhas e colunas identificam as zonas (centroides).

Modelos de Geração / Atração de Viagens

A primeira fase no modelo de quatro etapas é um processo de geração e atração de viagens para estimar o número de viagens que se originam e/ou terminam em cada zona. Esta fase do processo de estimativa de demanda de viagens pode ser realizada tanto no nível desagregado da família quanto no nível agregado das zonas, quando o número de viagens é assumido como uma função das características zonais. No que segue, restringiremos nossa descrição aos modelos agregados.

Cada zona de origem terá uma capacidade para geração de viagens que pode ser modelada em termos de suas características socioeconômicas (uso do solo, nível de renda, posse de veículos, emprego, etc.) como uma função:

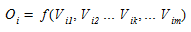(1.1)

onde \(O_{i}\) é o número de viagens geradas pela i-ésima zona e \(V_{ik}\) é a k-ésima variável socioeconômica da zona.

Da mesma forma, como um destino, cada zona, no nível agregado, terá uma capacidade para atração de viagens que também pode ser modelada como função de suas características socioeconômicas:

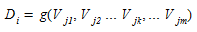(1.2)

onde, como antes, \(D_{j}\) é o número total de viagens atraídas pela zona \(j\), e \(v_{jk}\) é a k-ésima variável socioeconômica da zona \(j\).

No nível zonal agregado, as técnicas mais frequentemente utilizadas para geração e atração de viagens baseiam-se na análise de regressão múltipla, e então uma forma comum para as funções \(O_i\) e \(D_{j}\) poderia ser:

(1.3)

na qual os valores \(v_{ik}\) são os fatores de "produção" ou "atração" de viagens dados, dependendo do tipo de modelo, e os valores \(a_{ik}\) são os parâmetros cujos valores numéricos serão estimados por regressão múltipla após os dados disponíveis de pesquisas, bancos de dados censitários e outras fontes. Os fatores de geração/atração de viagens nessa abordagem podem ser zonas e atributos dos viajantes, assim como outros atributos como os modos de viagem, rotas de viagem, número de paradas de ônibus ou tempos e custos de viagem.

Modelos e Algoritmos de Distribuição de Viagens

A distribuição de viagens é o próximo passo na Metodologia de Quatro Etapas e é realizada após a geração/atração de viagens ser concluída. Consiste em distribuir entre vários destinos cada uma das origens de viagem Oi. Uma vez definido o conjunto de centroides, os movimentos desejados sobre a rede viária podem ser expressos em termos de uma matriz "origem-destino", cujas entradas especificam o fluxo (número de viagens durante o período de estudo) entre cada centroide de origem e cada centroide de destino na rede:

Matriz OD: T=\([t_{ij}]t_{ij}\) = número de viagens entre origem \(i\) e destino \(j\)

Levando em consideração a geração/atração de viagens de cada zona, a matriz de mobilidade, também chamada de matriz de viagens e matriz Origem-Destino, a matriz OD, que modela a demanda de transporte na área objeto de estudo, o problema de distribuição (Erlander e Stewart, 1990) trata de determinar uma matriz não negativa {\(t_{ij}\):} que satisfaça as restrições marginais:

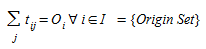
(EQN TD1)

e outras condições, como a soma das viagens que partem é igual à soma das chegadas:

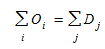(2.2)

A equação (2.1) significa que a soma das viagens geradas em cada origem sobre todos os destinos deve ser igual à capacidade de geração de viagens de cada origem, e a soma de todas as viagens que chegam a cada destino a partir de todas as origens deve ser igual à capacidade de atração de viagens de cada destino.

Três métodos para realizar os cálculos de distribuição de viagens estão disponíveis, um através de fatores de crescimento em matrizes de origem e destino utilizando técnicas de Furnessing, e dois em Modelagem de Demanda utilizando um Modelo de Gravidade ou um Modelo de Escolha de Destino.

Métodos de Fator de Crescimento (Furnessing)

Assumindo que uma matriz de viagens básica ou de referência {\(t_{ij}\)} de um estudo anterior ou pesquisa recente esteja disponível. O objetivo é estimar uma matriz de viagens {\(T_{ij}\)} para um ano de projeto usando informações disponíveis sobre a taxa de crescimento da área de estudo entre o ano da matriz de referência e o ano de projeto.

Neste caso, informações estão disponíveis sobre o número futuro de viagens que se originam e terminam em cada zona. Portanto, dois conjuntos de fatores de crescimento estão disponíveis para viagens de entrada e saída de cada zona: \(a_{i}\) e \(b_{j}\), respectivamente, de modo que:

(2.3)

Um modelo conhecido como o fator de crescimento duplamente restringido; o cálculo de {\(T_{ij}\)}, conforme definido por (2.3), satisfazendo as condições:

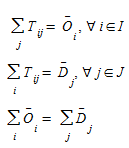(2.4)

Isso requer o cálculo dos coeficientes de crescimento \(a_{i}\) e \(b_{j}\), que é feito com o procedimento de balanceamento de Furness (Furness, 1965; veja também Fratar 1954, Bregman, 1967).

O procedimento de balanceamento de Furness é formulado da seguinte forma:

• Passo 0. Inicialização Defina l=0 (contagem de iterações), e 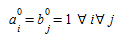(2.5)

• Passo 1. Balanceamento de linhas

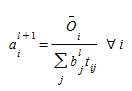
• Passo 2. Balanceamento de colunas

• Passo 3. Teste de Parada

O teste de convergência para o processo é

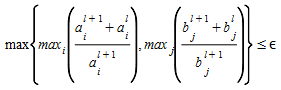
Se o erro aceitável ε for satisfeito ou l+1= lmax, (o número máximo de iterações foi atingido), então PARAR.

Caso contrário, defina l:=l+1 e retorne ao Passo 1.

Ortúzar e Willumsen apontam (Ortúzar e Willumsen, 1990) que os métodos de fator de crescimento são simples de entender e fazem uso direto de matrizes de viagens observadas e previsões de crescimento das extremidades de viagens. Isso também os limita a previsões de curto prazo, já que os métodos não levam em conta mudanças nos custos de transporte devido a alterações na rede. Também é importante notar que eles preservam os "zeros estruturais"; qualquer célula \(t_{ij}\) que é igual a zero na matriz OD do ano base, será igual a zero na matriz OD prevista \(T_{ij}\).

Métodos de Modelo de Demanda

Os Modelos de Gravidade pertencem à família de modelos projetados para prever padrões futuros de viagens quando mudanças significativas na rede ocorrem. Seu nome deriva da observação de que o volume de viagens tem alguma similaridade com a força da gravidade com uma razão direta à massa (ou população) de uma zona e uma razão inversa à distância entre zonas.

Os modelos de escolha de destino são um tipo de modelo de distribuição de viagens ou de interação espacial que são formulados como modelos de escolha discreta, tipicamente modelos logit, que atribuem viagens através de probabilidades maximizando a utilidade de cada viajante ao ir de cada origem a cada destino. A chave para este modelo é a suposição de que os viajantes selecionam seu destino com base na utilidade que ele tem para eles, enquanto tentam maximizá-la. Este modelo é reversível, com as mesmas utilidades, pode-se usar as viagens geradas (lado da partida) ou as viagens atraídas (lado da chegada) para fazer a atribuição de viagens.

Ao contrário do Modelo de Gravidade, o modelo de Escolha de Destino não corresponde automaticamente as viagens atribuídas aos vetores de Geração/Atração. No Aimsun Next, para resolver esse problema, preços sombra são adicionados às utilidades e calculados recursivamente. No entanto, esta é uma parte opcional que pode não ser necessária e, em alguns casos, até indesejável, pois distorce as utilidades modeladas pelo usuário.

Comparação entre o Modelo de Gravidade e o Modelo de Escolha de Destino

Uma comparação entre os dois modelos de demanda é mostrada nas tabelas abaixo. Observe que, enquanto o Modelo de Escolha de Destino oferece mais capacidade do que o Modelo de Gravidade, também requer um maior conhecimento dos fatores que controlam a demanda para utilizá-lo efetivamente. No entanto, note que ambos os modelos ainda omitem muitos atributos não observados ou não quantificados, como o preço e a qualidade dos bens e serviços fornecidos nos destinos, relacionamentos sociais, hábitos de viajantes e a estética de uma área.

Variáveis Observadas	Modelo de Gravidade/	Modelo de Escolha de Destino
Número de Domicílios	X	X
Número de funcionários por setor	X	X
Tempo de Viagem e/ou distância	X	X
Cruzamentos de rios, cruzamentos de rodovias e outras barreiras psicológicas conhecidas		X
Onde o viajante mora		X
Renda do viajante, etc.		X
Proximidade de destinos semelhantes e concorrentes		X
Comodidade dos destinos em relação a outros lugares atraentes		X
Caminhabilidade, densidade, mistura de usos nos destinos		X
Preços e Disponibilidade de Estacionamento (às vezes)		X

Nem todos os fatores que afetam a escolha podem ser medidos diretamente. Estes são inferidos por modelos.

Variáveis Não Observadas	Modelo de Gravidade/	Modelo de Escolha de Destino
Variação Aleatória Simples	X	X
Outras Atitudes/Preferências dos Viajantes (em relação ao preço e qualidade de bens/serviços, etc.)		X
Autocorrelação Espacial / Homogeneidade não observada dos destinos		X

Tabela derivada de Travel Forecasting Resource.

Modelo de Gravidade

A forma geral do modelo de gravidade é capturada na seguinte equação:

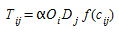(2.6)

onde \(O_i\), o número de viagens geradas pela origem \(i\) é a "massa" da origem \(i\), \(D_j\), a capacidade de atração de viagens do destino \(j\) é a "massa" do destino \(j\), α é uma constante e f(\(c_{ij}\)) é uma função de deterrência em termos do custo \(c_{ij}\) de viajar da origem \(i\) para o destino \(j\). A aplicação da fórmula (2.5) não pode ser imediatamente aplicada, pois a constante não pode ser determinada de tal maneira que as restrições marginais (2.1) e (2.2) sejam mantidas. Isso requer a introdução de fatores de normalização adicionais \(A_i\) e \(B_j\), e o modelo é reescrito na forma:

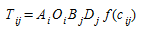(2.7)

Os vários tipos de modelos de gravidade são classificados pela forma da função de deterrência, os mais comuns são:

• Modelos de gravidade com função de deterrência exponencial
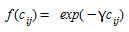
• Modelos de gravidade com função de deterrência de potência
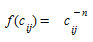
• Modelos de gravidade com função de deterrência combinada

Modelos de gravidade com uma Função de Deterrência Exponencial

Dada a natureza indeterminada do modelo, geralmente haverá um grande número de matrizes viáveis para um determinado conjunto de \(O_i\) e \(D_j\), porque existem \(i*j\) elementos e apenas i+j restrições nas equações (2.1). Isso implica que uma escolha entre as matrizes viáveis {\(T_{ij}\)} deve ser feita de acordo com algum critério adicional. A fim de levar em conta explicitamente os custos de viagem entre zonas quando \(c_{ij}\) do custo de viajar da zona i para a zona j para todas as zonas está disponível, o custo pode ser explicitamente incluído no modelo de entropia, acrescentando-o como uma restrição sobre a despesa total no sistema, quando custos generalizados são utilizados, ou totalizando o tempo de viagem no sistema quando custos são medidos em termos de tempos de viagem.

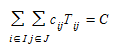
O modelo modificado agora é:

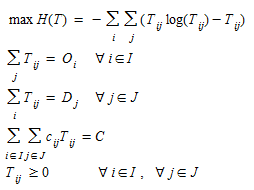(2.8)

que é novamente um modelo de otimização convexa cuja função Lagrangeana é:

(2.9)

onde, como antes, α\(_i\) e β\(_j\) são respectivamente os i-ésimo e j-ésimo multiplicadores de Lagrange da restrição em (2.8), γ é o multiplicador de Lagrange da restrição de tempo, e as condições de otimalidade são mantidas para:

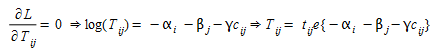(2.10)

Então, fazendo as mudanças,\(A_i\) \(O_i\)=exp{-α\(_i\)}, ∀ i ∈ I e \(B_j\) \(D_j\) = exp{-β\(_j\)}, ∀ j ∈ J a solução pode ser reescrita como:

(2.11)

E os coeficientes de balanceamento \(A_{i}\) e \(B_{j}\) podem ser calculados pelo seguinte algoritmo modificado de Furness:

Passo 0. Inicialização Defina l=0 (contagem de iterações), e \(A_i^0= B_j^0 =1\) , ∀ \(i\) , ∀ \(j\)

Passo 1. Balanceamento de linhas

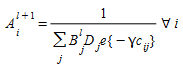
Passo 2. Balanceamento de colunas

Passo 3. Teste de Parada

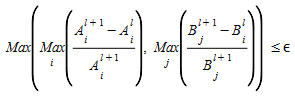
Se os critérios de convergência forem inferiores a ε ou l+1= lmax, (o número máximo de iterações) então PARAR. Caso contrário, defina l:=l+1 e retorne ao Passo 1.

Um valor estimado recomendado para o multiplicador de Lagrange γ é o inverso do custo médio de viagem entre zonas; ou seja, γ= (custo médio de viagem)^-1^.

Modelo de Escolha de Destino

O Modelo de Escolha de Destino calcula as probabilidades \(p_{ij}\) de atribuir viagens geradas na origem \(i\) (\(O_i\)) aos destinos \(j\):

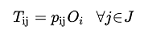(3.1)

Onde \(i,j\) são as zonas de origem e destino e \(O_i\) são as viagens geradas pela origem \(i\).

Para alcançar isso, um método de atribuição baseado na maximização da utilidade, utilizando um Modelo Logit Multinomial é usado com funcionalidade adicional (opcional) para igualar os valores de atração total por destino (\(A_j\)) calculados pela etapa de Geração/Atração aos atribuídos pelo cálculo da Escolha de Destino da Distribuição de Viagens. Note que este modelo também pode ser aplicado na direção oposta; usando valores de atração em vez de valores de geração:

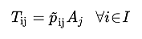(3.2)

Onde \(A_j\) são os valores atraídos e \( ilde{p}_{ij}\) é a probabilidade de um viajante com destino \(j\) partir da origem \(i\). Como a descrição deste problema simplesmente troca origens e destinos, sua descrição é omitida aqui.

Maximização da Utilidade e modelo de Escolha Logit Multinomial

O modelo de escolha de destino implementado no Aimsun Next utiliza um modelo de escolha logit multinomial, um modelo de maximização de utilidade para reproduzir as escolhas dos tomadores de decisão. Para mais detalhes sobre o modelo, consulte https://data.princeton.edu/wws509/notes/c6s3.

Primeiro, uma utilidade U é uma quantidade que mede "quão útil é uma escolha para o tomador de decisão em relação a outra ou outras" - portanto, a escolha a é preferida à escolha b se:

(3.3)

Neste caso, a e b são os pares origem-destino ij.

A partir da Eq.(3.3), fica claro que os valores relativos da utilidade são fundamentais; assume-se que o viajante escolherá a opção que maximiza sua utilidade. A partir dessa definição, a probabilidade de escolher a opção a ∈ A é:

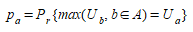(3.4)

No entanto, as utilidades estão sempre vinculadas a erros estatísticos nos atributos das escolhas, que se tornam:

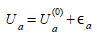(3.5)

Onde \(U^{(0)}_a\) é o valor exato da utilidade e (ε\(_a)\) é um termo de erro.

O Modelo Logit Multinomial assume que todos os erros são iguais e têm a seguinte distribuição:

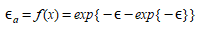(3.6)

Isso leva a:

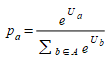(3.7)

Note que aqui, as decisões são baseadas apenas na utilidade de cada viajante individual, que são independentes das utilidades de outros viajantes. No entanto, como os viajantes interagem na rede de transporte, suas escolhas são afetadas pelas ações dos outros. Por exemplo, se um viajante for desestimulado pela lotação ou atrasos na opção a, sua decisão será afetada pelo número de outros viajantes que escolheram essa opção.

Escolhas de Probabilidade Zero

Em um Modelo de Escolha de Destino, modificar as utilidades para excluir uma ou mais opções enquanto se preserva as probabilidades das opções restantes pode ser programado. O processo é transformar as utilidades de tal forma que as seguintes afirmações sejam mantidas:

• As probabilidades das escolhas excluídas são zero: \(p_a = 0\) onde \(a\) é uma escolha excluída (par OD).
• As probabilidades entre as escolhas não excluídas devem ser invariantes para manter a ordem de preferências independentemente de outras opções.

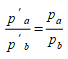(3.8)

A transformação é realizada até o limite das probabilidades quando as utilidades das escolhas excluídas vão para ∞. Esse limite significa que as escolhas excluídas nunca são preferidas a qualquer uma das escolhas não excluídas.

(3.9)

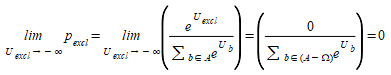(3.10)

Onde \(a\) é uma escolha não excluída do conjunto não excluído (A-Ω) e Ω é o conjunto de opções excluídas.

Numericamente, isso é equivalente a reescalar o denominador e configurar as probabilidades excluídas como zero, o que preserva a Eq.(3.8).

Modelo de Escolha de Destino com Restrições de Geração/Atração

O propósito deste método é impor as restrições de atração no Modelo de Escolha de Destino. Em geral, as viagens atribuídas a cada destino devem coincidir com os valores de atração calculados (notar que, porque \(p_{ij}\) são normalizadas, as gerações coincidem com as viagens atribuídas por construção). Assim, nesta seção, descreveremos o método para impor as seguintes restrições:

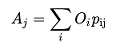(3.11)

Onde \(A_j\) é a atração do destino \(j\), \(O_i\) a geração pela origem \(i\) e \(p_{ij}\) é a probabilidade de um viajante ir de \(i\) para \(j\) que é dada por:

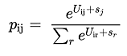(3.12)

Para impor todas as \(A_j\) restrições de atração, minimizamos uma métrica que considera o erro com o método de descida do gradiente modificando as utilidades:

onde \(s_j\) é o preço sombra.

A métrica é expressa como:

(3.13)

Onde τ\(_j\) são os pesos (opcionais) do destino \(j\). Note que a função \(F\) é convexa em relação a \(V_r\), mas não necessariamente em relação a \(s_j\).

Ao minimizar essa métrica, impomos que a atração seja igual ao número total de viagens atribuídas a cada destino, conforme na equação (3.11).

Utilizando a fórmula do método de descida do gradiente:

(3.14)

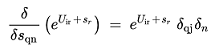(3.15)

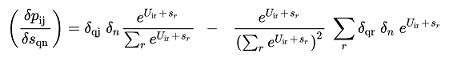3.(16)

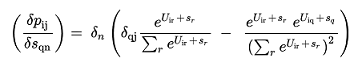(3.17)

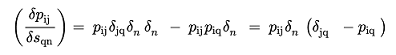(3.18)

Portanto:

(3.19)

Também pode ser reescrito como:

(3.20)

E finalmente, o algoritmo é, do passo \(k\) para \(k+1\):

(3.21)

Onde μ é o tamanho do passo (pequeno). μ também pode mudar entre os passos e será escolhido para minimizar F.

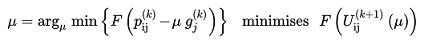(3.22)

Para encontrar o mínimo:

(3.23)

Porque \(s_j\) - μ\(g_j\) é convexa em μ, então, a função resultante também é convexa e os pontos estacionários também são mínimos e, portanto, mínimos globais. Para simplificar a notação \(V_r(0) = V_r\) e o ponto estacionário é um mínimo.

Portanto:

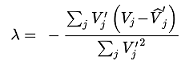(3.24)

Mínimos Locais

Há uma possibilidade de multiplicidade de pontos estacionários que podem ser mínimos, máximos ou um ponto de sela. A função a ser minimizada pode ser escrita como:

(3.25)

É evidente que possui apenas um ponto estacionário δF/δ\(V_j=0\) , um mínimo global quando \(hat{V}_j = V_j\) para todos \(j\). No entanto, em termos dos preços sombra \(V = V(s_q)\), não é necessariamente o único mínimo. Portanto, para determinar os pontos estacionários (máx, mín ou sela):

(3.26)

O método de descida do gradiente encontra um mínimo local por design, no entanto, não há como garantir, ou seja, com diferentes valores de \(A_j\) , \(O_i\) e \(p_{ij}(s_q = 0)\) que o mínimo encontrado seja global. Neste caso, \(dV_k/ds_q\) nunca se reduz a zero e, na prática:

(3.27)

Portanto, usando a Eq.(3.9), podemos encontrar para \(j = q\):

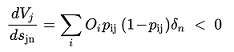(3.28)

E para \(j\) ≠ \(q\)

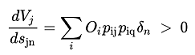(3.29)

Os únicos casos em que \(dV_k/ds_q\) desaparece são primeiro, quando todas as probabilidades de ir para o destino \(j\) \(p_{ij}\) são zero, exceto um valor, e o segundo caso quando \(p_{iq} = 0\). Nenhum desses é alcançado numericamente, pois correspondem a &\(s_q\) ± ∞.

Atribuição Estática de Tráfego: Modelos de Equilíbrio do Usuário

Os padrões de fluxo através de uma rede viária podem ser encarados como o resultado de dois mecanismos em competição:

• Os usuários do sistema tentam viajar de forma a minimizar a desutilidade associada ao transporte.

  • Motoristas dirigindo entre uma determinada origem e um determinado destino provavelmente escolherão a rota com o menor tempo de viagem.

• A desutilidade associada à viagem não é fixa, mas depende em parte da utilização do sistema de transporte.

  • O tempo de viagem em cada um dos caminhos conectando a origem e o destino é uma função do fluxo total de tráfego devido à congestão.

Consequentemente, pode não ser óbvio qual dos padrões de fluxo através da rede possui o menor tempo. A análise de transporte observa o nível de serviço do transporte (ou seu inverso, a desutilidade da viagem) e os fluxos. Os resultados da análise levam a um conjunto de fluxos e um conjunto de medidas de nível de serviço que estão em equilíbrio entre si.

O propósito do modelo é descrever a interação entre a congestão e as decisões de viagem que resultam nesse fluxo. Como a congestão aumenta com o fluxo e as viagens são desencorajadas pela congestão, essa interseção pode ser modelada como um processo que atinge um equilíbrio entre a congestão e as decisões de viagem.

A impedância da viagem, ou nível de serviço, associada às ligações que representam uma rede viária, pode incluir muitos componentes, refletindo tempo de viagem, segurança, custo da viagem, estabilidade do fluxo e outros. A representação mais comum dessa impedância é em termos de tempo de viagem, já que estudos empíricos parecem indicar que é um dos principais desestimulantes para o fluxo e, por outro lado, é mais fácil de medir do que muitos outros componentes potenciais de impedância. Como já mencionado, o nível de serviço nos serviços de transporte é geralmente uma função de seu uso. Devido à congestão, o tempo de viagem nas redes viárias é uma função crescente do fluxo. A representação típica da impedância de um link é em termos das chamadas funções "volume-atraso", expressando o tempo de viagem \(s_a(v_a)\) no link a∈A como uma função do volume \(v_a\) nesse link. Estas são funções não lineares cuja aparência teórica é semelhante à da figura abaixo, sempre abaixo da capacidade do link.

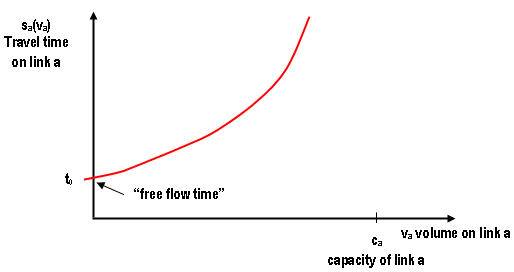
O conceito de equilíbrio na análise de transporte

É um conceito emprestado da teoria dos mercados perfeitamente competitivos modelados em termos de dois grupos interativos: os produtores e os consumidores. O comportamento dos produtores é caracterizado por uma função de oferta e o comportamento dos consumidores é caracterizado por uma função de demanda. A função de oferta expressa a quantidade de bens que o fornecedor produz em função do preço do produto. À medida que o preço aumenta, torna-se lucrativo produzir mais e a quantidade ofertada aumenta.

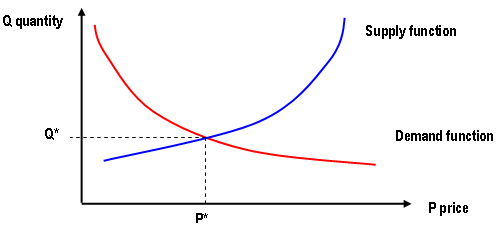
A função de demanda descreve o comportamento agregado dos consumidores ao relacionar a quantidade do produto consumido ao seu preço. À medida que o preço aumenta, a quantidade consumida diminui. A figura acima retrata funções simples de oferta e demanda para um determinado produto. O ponto em que as duas curvas se cruzam é caracterizado pelo preço "limpo de mercado", P^∗^, e pela quantidade produzida Q^∗^. O ponto (P^∗^,Q^∗^) é o ponto em que o preço permanece estável, conhecido como o ponto de "equilíbrio".

Para sistemas de transporte, a demanda é representada em termos de uma função de demanda que relaciona o número de viagens ao seu custo (ou seja, tempo de viagem) e a oferta é representada em termos de uma função de desempenho (ou seja, tempo de viagem entre pares OD), como na figura abaixo.

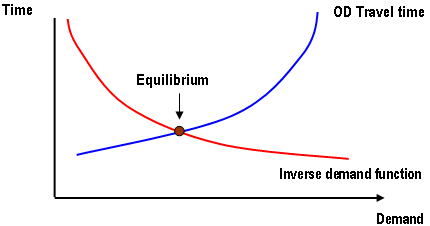
O equilíbrio do usuário é alcançado quando "nenhum viajante pode melhorar seu tempo de viagem mudando unilateralmente de rota" ou, como originalmente formulado por Wardrop (1952), "Os tempos de viagem em todas as rotas realmente usadas são iguais ou menores do que aqueles que seriam experimentados por um veículo em qualquer rota não utilizada", formulação conhecida como o primeiro princípio de Wardrop ou o princípio de Equilíbrio do Usuário de Wardrop.

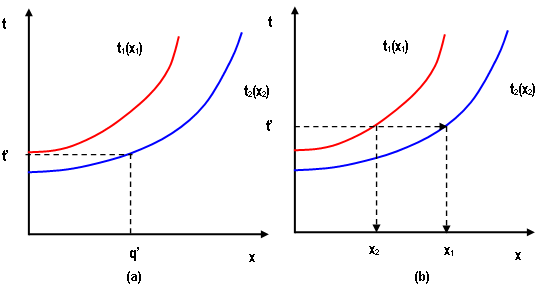
Um exemplo simples retirado de Sheffi (1985) ajudará a ilustrar e entender o Princípio de Wardrop. Considere uma rede simples como a da figura abaixo, com apenas uma origem e um destino conectados por duas rotas alternativas, com uma demanda total de \(q\) viagens, gerando os fluxos de tráfego \(x_1\) e \(x_2\), nas rotas um e dois, respectivamente, satisfazendo \(q = x_1+x_2\).

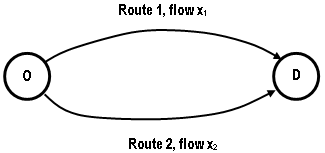
Suponha também que os tempos de viagem \(s_1\) e \(s_2\) nas rotas 1 e 2, respectivamente, são determinados pelas funções de desempenho \(s_1(x_1)\) e \(s_2(x_2)\) da figura abaixo, que estimam o tempo de viagem como função do fluxo de tráfego em cada rota.

Se o fluxo total é q < q’ , então tudo é atribuído à rota 2, cujo tempo de viagem é menor, como mostra a parte (a) da figura abaixo, mas para um fluxo maior \(q = x_1+x_2\), a distribuição de fluxo em equilíbrio, \(x_1\) e \(x_2\), entre as rotas 1 e 2 deve ser feita de tal forma que o tempo de viagem s em ambas as rotas seja o mesmo, como mostrado na parte (b) da figura abaixo.

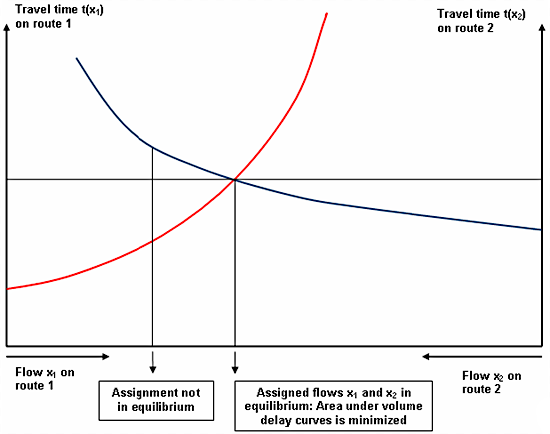
Outra maneira de visualizar o equilíbrio do usuário (EU), entre as duas rotas é sobrepor as duas curvas de custo (tempo de viagem ou volume de atraso) (Bell e Iida,(1997) como mostrado na figura abaixo. À esquerda da interseção das duas curvas, a rota 1 custa menos que a rota 2, e há um incentivo para mudar para a rota 1. À direita da interseção, a rota 2 custa menos que a rota 1, e há um incentivo para mudar para a rota 2. A interseção das duas curvas representa o ponto de equilíbrio em que os custos da rota 1 e 2 são iguais e não há incentivo para trocar de rotas. Geometricamente, a interseção também corresponde ao ponto que minimiza a área total sob as funções de custo; em qualquer outro ponto a área será maior.

Os principais modelos de tráfego para a estimativa da distribuição de fluxos de tráfego em uma rede viária são baseados em modelos matemáticos de escolha de rotas, ou seja, a modelagem de como os usuários escolhem suas rotas sob as condições de tráfego predominantes.

O conceito de equilíbrio desempenha um papel central neste processo de construção de modelos. Wardrop enunciou os dois princípios que formalizaram esse conceito de equilíbrio e introduziu o postulado comportamental da minimização dos custos totais, que junto com os princípios são as hipóteses fundamentais de modelagem. Os modelos de equilíbrio de tráfego são modelos descritivos que visam prever fluxos de links e tempos de viagem que resultam da forma como os usuários escolhem rotas de suas origens para seus destinos em uma rede de transporte (Florian, 1986, e Florian e Hearn, 1995) (Sheffi, 1985).

O primeiro princípio afirma que "Os tempos de viagem em todas as rotas realmente usadas são iguais ou menores do que aqueles que seriam experimentados por um único veículo em qualquer rota não utilizada".

Os fluxos de tráfego que satisfazem este princípio são geralmente referidos como "fluxos otimizados pelo usuário", pois cada usuário escolhe a rota que percebe como a melhor. "Fluxos otimizados pelo sistema" são caracterizados pelo segundo princípio de Wardrop, que afirma que "o tempo total de viagem é mínimo".

Modelos de Atribuição Estática de Tráfego construídos de acordo com esses princípios e o postulado da minimização do custo total, consideram um período específico de tempo para o qual as características da demanda foram determinadas e estimam os padrões de fluxo resultantes da interação da demanda e das características de congestão da infraestrutura de transporte disponível.

A rede viária é modelada em termos de um gráfico, cujos nós n ∈N representam origens, destinos e interseções de ligações, e ligações, a∈A representam a infraestrutura de transporte, como discutido acima. O fluxo de viagens em uma ligação a é dado por \(v_a\), e o custo de viajar em uma ligação é dado por uma função de custo do usuário \(s_a(v)\) onde \(v\) é o vetor de fluxos de ligações em toda a rede. Como essas funções modelam o tempo de atraso para uma jornada no arco \(a\), elas são chamadas de funções de volume/atraso. Uma hipótese chave de modelagem sobre o comportamento dessas funções é que se assume que elas são monotônicas, ou seja, tais que:

(4.1)

e também se presume que são contínuas e diferenciáveis.

A demanda de origem para destino, \(g_i\), i ∈* 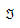, onde 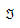é o conjunto de pares origem/destino, OD, pode usar caminhos direcionados \(k\), \(k\)∈\(K_i\), onde \(K_i\) é o conjunto de caminhos para o par OD \(i\). Os fluxos nos caminhos \(k\), \(h_k\), satisfazem as condições de conservação de fluxo e não negatividade:

(4.2)

Os correspondentes fluxos de ligação \(v_a\) são dados por:

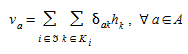(4.3)

Onde:

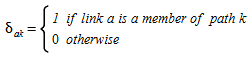
O custo de cada caminho \(s_k\) é a soma dos custos de usuário das ligações no caminho \(k\):

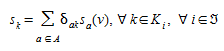(4.4)

Deixe \(u_i\) ser o custo do caminho de menor custo para qualquer par OD \(i\):

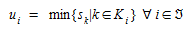(4.5)

O modelo de equilíbrio do usuário da rede, baseado no primeiro princípio de Wardrop, é formulado supondo que para cada par OD o princípio ótimo do usuário de Wardrop é satisfeito, ou em outras palavras, que todos os caminhos direcionados usados têm o mesmo custo, ou seja:

(4.6)

sobre o conjunto viável (4.2)-(4.3). Este modelo de equilíbrio de rede pode ser reescrito na forma de uma desigualdade variacional:

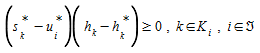(4.7)

onde \(h_k\) é qualquer fluxo de caminho viável. Se h^∗^~k~>0 , então s^∗^~k~=u^∗^~k~ porque \(h_k\) pode ser menor que h^∗^~k~, se h^∗^~k~=0 então a desigualdade é satisfeita quando s^∗^~k~-=u^∗^~k~≥0.

Somando sobre k∈K~i~, e i∈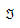, e levando em consideração as restrições (4.2) e (4.3) quando a demanda \(g_i\) é constante, o modelo (4.7) pode ser reformulado da seguinte forma (Fisk e Boyce, 1983) (Magnanti, 1984) (Dafermos, 1980):

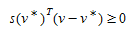(4.8)

que é a formulação da desigualdade variacional derivada por (Smith, 1979).

Modelos de Equilíbrio do Usuário com Demanda Fixa

Quando as funções de custo do usuário são separáveis, ou seja, elas dependem apenas do fluxo na ligação s~a~(v)= s~a~(v~a~)a∈A, e as demandas \(g_i\) são consideradas constantes, independentes dos custos de viagem, a formulação da desigualdade variacional possui o seguinte problema de otimização convexa equivalente (Patriksson, 1994; Florian e Hearn, 1995):

(4.9)

e a restrição definicional de \(v_a\) (4.3).

Embora o problema de atribuição de tráfego seja um caso especial de fluxos de rede não lineares de múltiplas mercadorias, e possa ser resolvido por qualquer um dos métodos usados para a solução desse problema, algoritmos mais eficientes para resolver esse problema, baseados em uma adaptação do método de aproximação linear de Frank e Wolfe (Frank e Wolfe, 1956) foram desenvolvidos nos últimos anos (Leblanc et al., 1975) (Nguyen, 1976) (Florian, 1976). Outros algoritmos eficientes baseados na abordagem simplicial restrita foram desenvolvidos por Hearn et al. (Lawphongpanich e Hearn, 1982) (Guélat, 1982) ou em uma adaptação do método de tangentes paralelas (PARTAN) (Florian et al., 1987).

A adaptação do método de aproximação linear para resolver o problema de atribuição de equilíbrio do usuário requer apenas o cálculo de caminhos mais curtos e uma minimização unidimensional de uma função convexa. Começando a partir de uma solução viável, o método de aproximação linear gera uma direção de descida viável (Bazaraa et al, 1993; Sheffi, 1985) resolvendo um subproblema que é obtido linearizando a função objetivo. Então, uma solução aprimorada é encontrada ao longo do segmento de linha entre a solução atual e a solução do subproblema. Para a EU com demandas fixas formuladas em (4.9), onde as funções de custo são separáveis, a aproximação linear da função objetivo em uma iteração intermédia l, quando a solução atual \(v^{(l)}\) é:

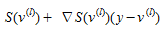(4.10)

Como \(S(v^{(l)})\) e ∇S(v^(l)^)(v^(l)^) são constantes, o subproblema linearizado a ser resolvido reduz-se a:

(4.11)

mudando a ordem de soma na função objetivo (4.11) e usando (4.4) o objetivo se torna:

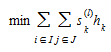(4.12)

Uma vez que os termos da função objetivo (4.12) podem ser separados agora por par OD \(i\), a solução do subproblema linearizado pode ser obtida calculando o caminho mais curto para cada par OD i, e alocando a demanda \(g_i\) às ligações desses caminhos. Tal alocação ou atribuição de demanda é referida como uma atribuição "tudo ou nada". Isso produz o vetor de fluxo de arco:

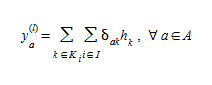(4.13)

e a direção de descida é:

(4.14)

Uma iteração do algoritmo de aproximação linear é concluída encontrando a solução de

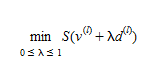(4.15)

ou, equivalentemente, anulando sua derivada, ou seja, encontrando &lambda; onde 0≥λ≥1, para o qual

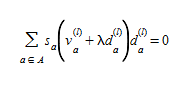(4.16)

a menos que o mínimo de (4.14) seja atingido para λ=0 ou λ=1.

A principal vantagem computacional do método de aproximação linear é que os caminhos que são usados em cada iteração para calcular a direção de descida são gerados conforme necessário e não precisam ser mantidos em iterações sucessivas. Isso significa que os requisitos de armazenamento não aumentam com o número de iterações. Em cada iteração, apenas os fluxos \(v^{(l)}\) e os custos de ligação \(s^{(l)}\) precisam ser mantidos, além dos dados da ligação da rede.

Como \(S(v)\) é uma função convexa e ∇S(v)=s(v),

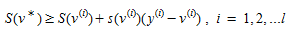(4.17)

O lado direito da (4.17) fornece um limite inferior sobre os valores ótimos S(v^∗^) em cada iteração. O melhor limite inferior obtido até a iteração atual \(l\) é:

(4.18)

Daí, um critério de parada natural, geralmente denotado como a lacuna relativa (RGAP) é

(4.19)

Falando de forma geral, todas essas adaptações do método de aproximação linear (LAM) estão dentro da seguinte estrutura algorítmica (Florian, 1986; Florian e Hearn, 1995), que é a usada para a função de Atribuição de Tráfego no Aimsun Next:

PASSO 1: Inicialização: Encontre uma solução inicial viável \(v^{(1)};s^{(1)}=s(v^{(1)});l=1\)

PASSO 2: Solução do subproblema linearizado na iteração l

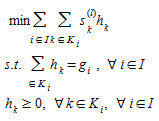
onde \(s^{(l)}_k\) é o custo no caminho k na iteração l. Para cada par OD \(i\) o algoritmo encontra o caminho mais curto \(k\)^∗*\(_i\) e realiza uma atribuição tudo ou nada, encontra os fluxos \(h^{(l)}_k\), calcula o vetor de fluxo de arco \(y^{(l)}\) de acordo com (4.12), e a direção de descida \(d^{(l)}=y^{(l)}-v^{(l)}\) de acordo com (4.13)

PASSO 3: Verifique se um critério de parada pré-determinado é satisfeito (ou seja, RGAP≤ε). Se for satisfeito, então PARAR; caso contrário, continue para o Passo 4.

PASSO 4: Encontre o tamanho do passo ótimo λ^(l)^ resolvendo (4.15)

PASSO 5: Atualize os fluxos e custos de ligação

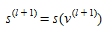
Defina \(l=l+1\) e retorne ao Passo 2.

A lenta convergência do método de aproximação linear na vizinhança da solução ótima levou à investigação de variantes do método, que poderiam melhorar a taxa de convergência, mantendo a simplicidade e as vantagens computacionais das aproximações lineares.

Um método de aceleração da convergência próximo à solução ótima é a mudança da direção de descida, como explicado em

Copyright © Aimsun SLU

Made with Material for MkDocs