Ajuste Estático de Saída OD

Algoritmos de Ajuste Estático de Saída

O método de ajuste estático de saída OD foi desenvolvido como uma melhoria para o fatiamento da matriz original em que a demanda de tráfego dinâmica é obtida fatiando o tempo de simulação em um número de períodos e, em seguida, cada fatia é ajustada de forma independente.

Este método funciona bem se os tempos de viagem entre a origem e o destino são curtos em relação ao período, mas mostra um viés no tempo de saída para viagens mais longas porque o aspecto do tempo de viagem é negligenciado. O ajuste estático de saída resolve esse problema ao levar em conta o tempo de viagem obtido a partir da alocação estática no cálculo da demanda de tráfego dinâmica.

Definição do Problema

O objetivo é encontrar uma demanda dinâmica x que minimiza a soma das distâncias quadradas entre as contagens observadas yˆ e as contagens simuladas y, com a matriz de alocação A e y = Ax isso pode ser escrito como:

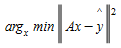
Para construir a matriz de alocação que mapeia a demanda dinâmica para as contagens observadas, as seguintes suposições são feitas:

• Os tempos de viagem dos segmentos são constantes durante o período de simulação.
• A escolha do caminho é constante durante o período de simulação.
• A demanda é gerada uniformemente durante cada fatia de tempo.

As seguintes definições são usadas:

• \(x_{0}\) é um vetor contendo viagens para cada origem \(a\) para destino \(b\): \(x_{0ab}\).
• \(I\) são os intervalos, que podem ser intervalos de partida ou de detecção, dependendo do que referenciam.
• \(D\) é a duração da fatia de tempo (intervalo).
• \(C\) é o conjunto de segmentos com contagens.
• \(x\) é um vetor contendo proporções de viagem para cada origem \(a\) para destino \(b\) para cada intervalo de partida \(d\): \(x_{abd}\).
• \(yˆ\) é um vetor contendo contagens observadas para cada segmento \(c\) para cada intervalo de detecção \(e\): \(yˆ_{ce}\)
• \(y\) é um vetor contendo volumes simulados para cada segmento \(c\) para cada intervalo de detecção \(e\): \(y_{ce}\)
• \(K_{ab}\) é o conjunto de caminhos usados de \(a\) para \(b\).
• \(t_{kc}\) é o tempo de viagem para o segmento \(c\) usando o caminho \(k\).
• \(p_{k}\) é a proporção de uso para o caminho \(k\).

Cada célula da matriz \(A\) pode ser construída com:

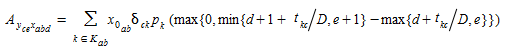
onde:

Baseado no cálculo da fração de demanda de um par OD partindo no intervalo \(d\) que passa por um ponto de detecção no intervalo \(e\).

Exemplo:

Neste exemplo, o tempo para viajar da origem \(a\) para o segmento \(c\) pelo caminho \(p\) é 0,75D, então 25% da demanda gerada no intervalo 1 passa pelo segmento \(c\) no intervalo 1 e 75% da demanda gerada no intervalo 1 passa pelo segmento \(c\) no intervalo 2.

Conservação da Demanda

O objetivo do ajuste estático de saída é calcular a demanda dinâmica a partir de uma demanda estática, portanto, é desejável que as viagens OD sejam conservadas e apenas distribuídas no tempo. Para obter isso, as seguintes equações são adicionadas à definição original do problema:

Significando que as frações para todos os intervalos de um determinado par OD devem somar 1, de modo que o fluxo OD seja preservado.

Resultado

As equações para a matriz de alocação e a conservação da demanda são um sistema linear de equações que podem ser prontamente resolvidas em um sentido de mínimos quadrados com métodos de soluções padrão, como métodos de descida de gradiente. Multiplicando a demanda original pelas frações calculadas x fornece a demanda dinâmica.

Exemplo

Considere a seguinte rede exemplo para ilustrar o processo.

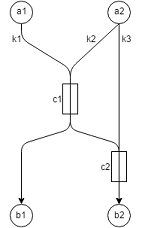
Existem dois pares OD; \(a1-b1\) usando o caminho \(k1\) e \(a2-b2\) usando 33% do caminho \(k2\) e 67% do caminho \(k3\). O caminho \(k1\) passa pelo ponto de detecção \(c1\), o caminho \(k2\) passa pelos pontos de detecção \(c1\) e \(c2\), e o caminho \(k3\) passa pelo ponto de detecção \(c2\).

Os tempos de viagem são:

• de \(a1\) para \(c1\) usando o caminho \(k1\): 5 minutos
• de \(a2\) para \(c1\) usando o caminho \(k2\): 5 minutos
• de \(a2\) para \(c2\) usando o caminho \(k2\): 10 minutos
• de \(a2\) para \(c2\) usando o caminho \(k3\): 5 minutos.

O tempo de simulação é de 45 minutos dividido em três intervalos de 15 minutos (\(i1\), \(i2\), \(i3\)). Durante esses 45 minutos, 1000 veículos vão de \(a1\) para \(b1\) e 1200 veículos vão de \(a2\) para \(b2\). Finalmente, as contagens observadas para os dois detectores são:

• \(c1\): (180, 520, 530)
• \(c2\): (130, 500, 450)

Então:

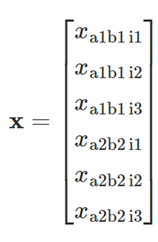
e

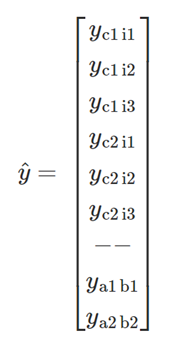
Em que \(y_{a1b1}\) e \(y_{a2b2}\) são iguais a um refletindo que a demanda deve ser conservada. Agora podemos calcular a matriz A calculando a matriz de alocação e adicionando as equações para conservação da demanda:

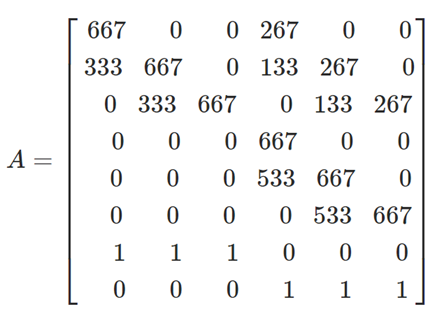
Os dados observados + equações de conservação da demanda dão:

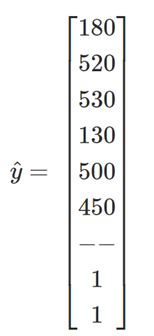
A solução é então dada por:

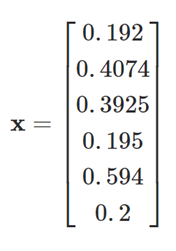
A partir da qual as viagens dinâmicas OD podem ser obtidas facilmente multiplicando os fatores pelo volume OD original, dando:

• \(a1-b1\): (192, 407, 393)
• \(a2-b2\): (234, 712, 240)